Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 55
O dispositivo mostrado é usado para ajuste grosseiro da altura de um aparato experimental sem uma mudança em sua posição horizontal. Por causa da junta corrediça em A, girar o parafuso não gira a perna cilíndrica acima de A. O diâmetro médio da rosca é 3/8 pol. E o coeficiente de atrito é 0,15. Para um projeto conservador que despreza o atrito na junta deslizante, qual deve ser o número mínimo N de roscas por polegada para garantir que o parafuso de rosca única não gire sozinho sob o peso do aparelho?
Passo 1
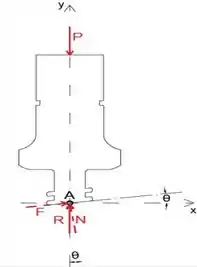
Primeiro, vamos desenhar o diagrama de corpo livre do dispositivo
Para que o dispositivo esteja em equilíbrio, a força resultante R precisa ser vertical, ou seja, a rosca precisa fazer o ângulo θ com o eixo x
Como sabemos o coeficiente de atrito, podemos calcular o ângulo máximo que fornecerá o equilíbrio θ
Passo 2
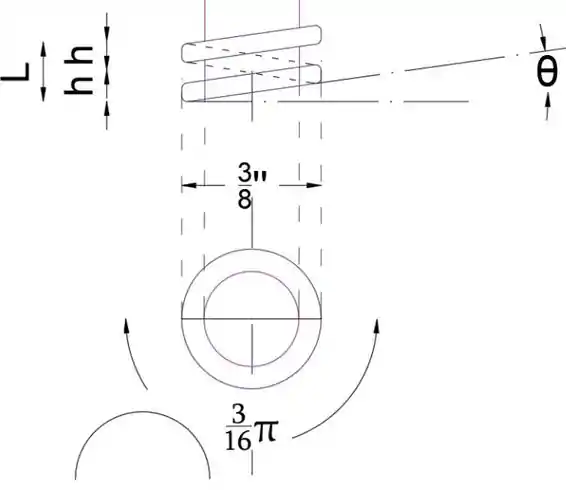
A seguir, vamos ampliar os tópicos
O comprimento do semicírculo de 3/8 pol. De diâmetro é
Como sabemos o ângulo máximo θ, podemos determinar a altura máxima da rosca
Passo 3
Uma vez que calculamos a altura máxima do fio, é fácil determinar o número mínimo de fios por polegada