Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 84

A trajetória do movimento de uma partícula de 5 kg no plano horizontal é descrita em termos das coordenadas polares como r = ( 2 t + 1 ) m e θ = ( 0,5 t 2 - t ) , onde t é dado em segundo. Determine a intensidade da força resultante atuando sobre a partícula quando t = 2 s.

Passo 1

O enunciado nos dá as seguintes informações:

Massa da partícula: m = 5 kg

Trajetória no plano horizontal;

Coordenadas polares.

Como a trajetória está no plano horizontal, a coordenada em z será desprezada pois não afetará o cálculo do problema. Desenhamos o diagrama de corpo livre da partícula.

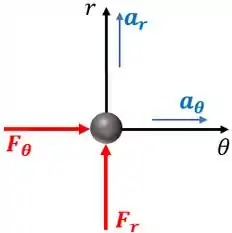
Sabemos que a trajetória do movimento é descrita por:

r = ( 2 t + 1 )

θ = ( 0,5 t 2 - t )

A partir desses dados, devemos determinar a intensidade da força resultante F sobre a partícula quando t = 2 s.

Passo 2

Primeiramente, vamos encontrar as derivadas temporais de r ( r ˙ e r ¨ ):

r ˙ = d r d t = 2   m / s

r ¨ = d 2 r d t 2 = 0   m / s 2

Em seguida encontraremos as derivadas temporais de θ ( θ ˙ e θ ¨ ):

θ ˙ = d θ d t = t - 1   r a d / s

θ ¨ = d 2 θ d t 2 = 1   r a d / s 2

Passo 3

Substituindo t = 2 s nas equações encontradas, temos que

r = 2 t + 1 = 5   m

r ˙ = 2   m / s

r ¨ = 0   m / s 2

θ = 0,5 t 2 - t = 0   r a d

θ ˙ = t = 1   r a d / s

θ ¨ = 1   r a d / s 2

Passo 4

Sabemos que as componentes da aceleração nas coordenadas r e θ são dadas por

a r = r ¨ - r θ ˙ 2

a θ = r θ ¨ + 2 r ˙ θ ˙

Logo, em t = 2

a r = r ¨ - r θ ˙ 2 = 0 - 5 1 2 = - 5   m / s 2

a θ = r θ ¨ + 2 r ˙ θ ˙ = 5 1 + 2 2 1 = 9   m / s 2

O sinal negativo de a r nos diz que esta aceleração está atuando no sentindo oposto ao qual desenhamos no diagrama de corpo livre.

Passo 5

Agora aplicaremos as Equações do Movimento para resolver o problema.

Analisando primeiramente no eixo r , temos que

∑ F r = m a r

F r = 5 - 5 = - 25   N

O sinal negativo de F r nos diz que a força está atuando no sentindo oposto ao qual desenhamos no diagrama de corpo livre.

Analisando no eixo θ , temos

∑ F θ = m a θ

F θ = 5 9 = 45   N

Passo 6

Sabemos que

F = F r 2 + F θ 2

Logo

F = - 25 2 + 45 2 = 51,48   N

Resposta

F = 51,48   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que o momento angular por unidade de massa h de um satélite que descreve uma órbita elíptica de semieixo maior a e excentricidade ε , em torno de um planeta de massa M, pode ser expresso como h
Um satélite descreve uma órbita elíptica em torno de um planeta. Representando por r0 e r1 as distâncias correspondentes, respectivamente, ao perigeu e ao apogeu da órbita, mostre que a curvatura da ó
Uma partícula de massa m descreve uma trajetória definida pela equação r = r 0 sen θ sob uma força central F voltada para o centro de força O. Mostre que F é inversamente proporcional àquinta potência
Uma partícula de massa m é lançada do ponto A com uma velocidade inicial v 0 perpendicular a OA e se move sob a ação de uma força central F ao longo de uma trajetória elíptica definida elaequação r =
Uma partícula de massa m descreve uma cardioide r = r 0 (1 cos θ /2) sob uma força central F voltada para o centro de força O. Usando a Eq. (12.37), mostre que F é inversamente proporcional ao quadrad