Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 54

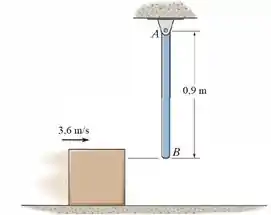
A barra A B de 2 kg está pendurada na posição vertical. Um bloco de 1 k g , deslizando sobre uma superfície horizontal lisa com uma velocidade de 3,6   m / s , acerta a barra na sua extremidade B. Determine a velocidade do bloco imediatamente após a colisão. O coeficiente de restituição entre o bloco e a barra em B é e = 0,8 .

Passo 1

O momento de inércia da barra A B em torno do ponto A é calculado por

I A = 1 12 m b r L 2 + m b r d 2

I A = 1 12 2 0,9 2 + 2 0,45 2

I A = 0,54   k g . m 2

E a velocidade angular da barra após a colisão é dada por

( ω b r ) 2 = ( v b r ) 2 r b r

Passo 2

Como o momento angular do sistema em torno do ponto A é conservado, temos:

( H A ) 1 = ( H A ) 2

[ m b l v b l ) 1 r b r = I ω b r 2 + [ m b l v b l ) 2 r b r

Logo,

1 3,6 0,9 = 0,54 ( v b r ) 2 0,9 + 1 ( v b l ) 2 0,9       e q . 1

Passo 3

Em virtude da colisão entre o bloco e barra deve-se aplicar a equação do coeficiente de restituição. Dessa forma, temos:

e = ( v b r ) 2 - ( v b l ) 2 ( v b l ) 1 - ( v b r ) 1

0,8 = ( v b r ) 2 - ( v b l ) 2 3,6 - 0       e q . 2

Resolvendo o sistema formado pelas equações (1) e (2), obtemos:

( v b r ) 2 = 3,888   m / s

E

( v b l ) 2 = 1,008   m / s

Resposta

A velocidade do bloco após a colisão é igual a 1,008   m / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um satélite de massa 700k g é lançado em uma trajetória de voo livre em torno da Terra a uma velocidade inicial v A = 10k m / s , quando a distância do centro da Terra é r A = 15M m . Se o ângulo de l
No instante que r = 1,5m , ao disco de 5k g é dada uma velocidade v = 5 m / s , perpendicular à corda elástica. Determine a velocidade do disco e a taxa de encurtamento da corda elástica no instante r
A bola de 2k g gira em torno de uma trajetória circular de 0,5m de diâmetro com velocidade constante. Se o comprimento da corda é encurtado de l = 1m até l ' = 0,5m , puxando-se a corda através do tub
Quando se dá ao pêndulo de 2k g uma velocidade horizontal de 1,5m / s , ele começa a girar em torno da trajetória circular horizontal A . Se a força F na corda é aumentada, o pêndulo sobe, e então gir
O barco-bombeiro descarrega dois jatos de água do mar, cada um com vazão de 0,25m 3 / s a uma velocidade de saída de 50m / s . Determine a tração desenvolvida na corrente da âncora, necessária para se