Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 104
No instante que , ao disco de é dada uma velocidade , perpendicular à corda elástica. Determine a velocidade do disco e a taxa de encurtamento da corda elástica no instante . O disco desliza sobre o plano horizontal liso. Despreze sua dimensão. A corda tem um comprimento não deformado de .
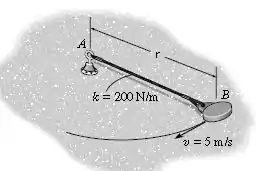
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Por conservação de energia, temos:
Aplicando conservação de quantidade de movimento angular, temos:
Portanto, podemos encontrar a velocidade radial por:
Resposta
Exercícios de Livros Relacionados
A esfera de 0,7k g se desloca em um plano horizontal e é controlada por um cordão que oscila para dentro e para fora da mesa de tal forma que o centro da esfera está limitado à trajetória dada por x 2
Uma pequena partícula de 110g é projetada com uma velocidade horizontal de 2m / s no topo A da guia circular lisa fixada no plano vertical. Calcule a taxa de variação no tempo H B ˙ da quantidade de m
Cada uma das cinco partículas conectadas possui uma massa de 0,6k g , com G como o centro de massa do sistema. Em um determinado instante a quantidade de movimento angular do sistema em torno de G é 1
As quatro esferas de 3k g estão rigidamente montadas na estrutura e eixo com rotação, que estão inicialmente girando livremente em torno do eixo vertical z na velocidade angular de 20r a d / s no sent
Uma centrífuga é constituída por quatro recipientes cilíndricos, cada um com massa m , a uma distância radial r a partir do eixo de rotação. Determine o tempo t necessário para levar a centrífuga a um