Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 100

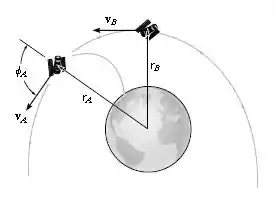
Um satélite de massa 700   k g é lançado em uma trajetória de voo livre em torno da Terra a uma velocidade inicial v A = 10   k m / s , quando a distância do centro da Terra é r A = 15   M m . Se o ângulo de lançamento nesta posição pe ϕ A = 70 ° , determine a velocidade v B do satélite e sua distância mais próxima, r B do centro da Terra. A Terra tem uma massa M e = 5,976 10 24 k g . Dica: sob estas condições, o satélite está sujeito apenas à força gravitacional da Terra, F = G M e m s / r 2 (Equação 13.1). Para obter parte da solução use a conservação de energia.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos aplicar o principio da conservação de quantidade de movimento angular:

H O 1 = H O 2

r 1 m v 1 = r 2 m v 2

m s v A sin ⁡ ϕ A r A = m s v B r B

700 10 10 3 sin ⁡ 70 ° 15 10 6 = 700 ( v B ) ( r B )

v B r B = 1,41 ( 10 11 )

r B = 1,41 10 11 v B

Vamos aplicar a conservação de energia entre o ponto A e B , para descobrir a velocidade no ponto B :

T A + V A = T B + V B

1 2 m s v A 2 - G M e m s r A = 1 2 m s v B 2 - G M e m s r B

1 2 700 10 10 3 sin ⁡ 70 ° 2 - 66,73 10 - 12 5,976 10 24 700 15 10 6 = 1 2 ( 700 ) v B 2 - 66,73 10 - 12 5,976 10 24 700 r B

Podemos substituir r B = 1,41 10 11 v B , assim obteremos uma equação do segundo grau. Ao resolvê-la, teremos:

v B = 10,2   k m / s

r B = 13,8   M m

Resposta

v B = 10,2   k m / s

r B = 13,8   M m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No ponto A de maior aproximação com o Sol, um cometa tem uma velocidade v A = 57,45 10 3 m / s . Determine as componentes radial e transversal de sua velocidade v B no ponto B, onde a distância radial
A partícula de 0,02k g se desloca ao longo da trajetória tracejada mostrada e tem as velocidades indicadas nas posições A e B . Calcule a média no tempo do momento em torno de O da força resultante P
As duas esferas de massas iguais m podem deslizar ao longo da haste horizontal que gira. Se elas estão inicialmente travadas na posição a uma distância r do eixo de rotação com o conjunto girando livr
Uma partícula é liberada na parede interna lisa de um reservatório cilíndrico em A com uma velocidade v 0 que faz um ângulo β com a tangente horizontal. Quando a partícula atinge um ponto B uma distân
O conjunto de duas esferas de 5k g está girando livremente em torno do eixo vertical a 40r p m com θ = 90 ° . Se a força F que mantém a determinada posição é aumentada para elevar o cursor da base e r