Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 107

Quando se dá ao pêndulo de 2   k g uma velocidade horizontal de 1,5   m / s , ele começa a girar em torno da trajetória circular horizontal A . Se a força F na corda é aumentada, o pêndulo sobe, e então gira em torno da trajetória circular horizontal B . Determine a velocidade do pêndulo em torno da trajetória B . Além disso, descubra o trabalho realizado pela força F .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos imaginar um diagrama de corpo livre para a situação e ver como as forças se comportam:

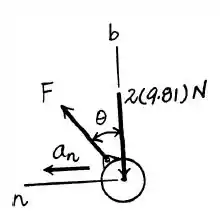
Temos que:

∑ F b = 0

F cos ⁡ θ - 2 9,81 = 0

∑ F n = m a n

F sin ⁡ θ = 2 v 2 l sin ⁡ θ

Vamos às relações trigonométricas:

sin 2 ⁡ θ cos ⁡ θ = v 2 9,81 l

1 - cos 2 ⁡ θ cos ⁡ θ = v 2 9,81 l

Aplicando aos valores do problema, temos:

1 - cos 2 ⁡ θ 1 cos ⁡ θ 1 = 1,5 2 9,81 ( 0,6 )

cos 2 ⁡ θ 1 + 0,3823 cos ⁡ θ 1 - 1 = 0

Resolvendo essa equação do segundo grau, teremos que:

θ 1 = 34,21 °

Vamos aplicar conservação de quantidade de movimento angular para relacionar os dois momentos:

H z 1 = H z 2

r 1 m v 1 = r 2 m v 2

0,3373 ( 2 ) ( 1,5 ) = 0,3 sin ⁡ θ 2 2 v 2

v 2 sin ⁡ θ 2 = 1,6867

1 - cos 2 ⁡ θ 2 cos ⁡ θ 2 = v 2 2 9,81 ( 0,3 )

θ 2 = 57,866 °

v 2 = 1,99   m / s

Aplicando conservação de energia e trabalho, temos:

T 1 + ∑ U = T 2

1 2 m v 1 2 + U F + - W h = 1 2 m v 2 2

1 2 2 1,5 2 + U F - 2 9,81 0,3366 = 1 2 2 1,992 2

U F = 8,32   N ⋅ m

Resposta

v 2 = 1,99   m / s

U F = 8,32   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As duas pequenas esferas, cada uma com massa m , estão conectadas por um cordão de comprimento 2 b (medido até os centros das esferas) e estão inicialmente em repouso sobre uma superfície horizontal l
Uma corda flexível inextensível de massa ρ por unidade de comprimento e comprimento igual a 1 / 4 da circunferência do tambor fixo de raio r é liberada a partir do repouso na posição horizontal tracej
As três pequenas esferas, cada uma com massa m , estão presas às hastes leves de modo a formar uma unidade rígida apoiada no plano vertical pela superfície circular lisa. A força de módulo constante P
A bola de golfe de 0,05k g é atingida pelo taco e desloca-se ao longo da trajetória mostrada. Determine a força impulsiva média que o taco transmite à bola, se o taco mantém contato com a bola durante
A bola de beisebol de 0,15k g tem uma velocidade de v = 30m / s , imediamente antes de ser atingida pelo taco. Após isso, ela desloca-se ao longo da trajetória mostrada, antes que o apanhador a pegue.