Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 67

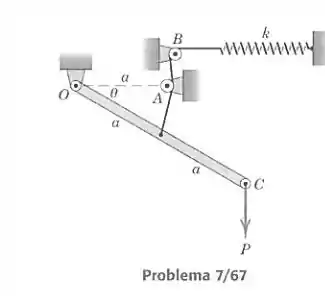
A barra leve O C é articulada em O e balança no plano vertical. Quando θ = 0 , a mola de rigidez k não está alongada. Determine o ângulo de equilíbrio, correspondente a uma força vertical P aplicada à extremidade da barra. Despreze a massa da barra e o diâmetro das pequenas polias.

Passo 1

Pelo princípio do trabalho virtual, ao deslocarmos o sistema girando a barra O C de um ângulo infinitesimal δ θ , o trabalho virtual total realizado pelas forças ativas deve ser igual à variação de energia potencial:

δ U = δ V

A única força ativa externa ao sistema (força que realiza trabalho) é a força P , e desprezando as massas, a força potencial toda é dada pela mola. Então vamos calcular δ U da força e δ V da mola para um pequeno giro da barra, e então igualar.

Passo 2

Primeiro vamos calcular o trabalho virtual δ U . A distância vertical do ponto C até O é dada por:

h = 2 a sen ⁡ θ

Por derivação relacionamos a variação infinitesimal δ h da altura com a do ângulo:

δ h = 2 a cos ⁡ θ δ θ

O trabalho realizado pela força é a força vezes o deslocamento:

δ U = P   δ h = 2 a P cos ⁡ θ δ θ

Passo 3

Agora vamos calcular a variação δ V da energia potencial da mola. Para θ = 0 a mola está relaxada, então todo o elongamento adicional x da mola tem o tamanho da parte da cordinha abaixo de A :

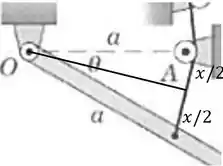
O alongamento x então é calculado através do ângulo θ 2 :

sen ⁡ θ 2   = x 2 a ⇒ x = 2 a sen ⁡ θ 2

Então a energia potencial da mola em função de θ é:

V = 1 2 k x 2 = 1 2 k ⋅ 4 a 2 sen 2 ⁡ θ 2 = 2 k a 2 sen 2 ⁡ θ 2

Derivando, chegamos à variação infinitesimal da energia potencial:

δ V = 2 k a 2 sen ⁡ θ 2 cos ⁡ θ 2 δ θ

Como 2 sen ⁡ θ 2 cos ⁡ θ 2 = sen ⁡ θ :

δ V = k a 2 sen ⁡ θ δ θ

Passo 4

Agora usamos o Princípio do Trabalho Virtual:

δ U = δ V

⇒ 2 a P cos ⁡ θ δ θ = k a 2 sen ⁡ θ δ θ

Cortando δ θ e isolando sen ⁡ θ / cos ⁡ θ :

⇒ tan ⁡ θ = 2 a P k a 2 = 2 P k a

⇒ θ = arctan ⁡ 2 P k a

Resposta

θ = arctan ⁡ 2 P k a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

27- O projeto existente de um carrinho para colocação de carga em aviões está sob revisão. A plataforma A D do carrinho é elevada até a altura adequada pelo mecanismo mostrado. Existem dois sistemas d
70- Duas cascas semicilíndricas com retângulos projetados iguais são formadas de lâminas metálicas, uma com a configuração a ) e a outra com configuração b ) . Ambas as cascas repousam sobre uma super
A caixa de 200k g está no elevador pantográfico na posição θ = 30 ° . Determine a força no cilindro hidráulico A D para equilíbrio. Despreze a massa dos componentes da plataforma elevatória.
A barra uniforme AO tem um peso de 50 N. Quando a barra está na posição vertical, θ=0º, a mola está livre. Determine o ângulo θ para o equilíbrio se a extremidade da mola contorna a periferia do disco
O ‘pantógrafo de Nuremberg’ está sujeito a uma força horizontal P=600 N. Determine o ângulo θ para o equilíbrio. A mola tem uma rigidez k = 15 kN/m e está livre quando θ=15º