Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 32
Determine a coordenada x do centroide do segmento esférico sólido.
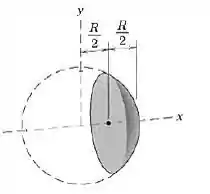
Passo 1
Sabendo que as equações para encontrar o centroide é dado por:
Dessa maneira, vamos primeiro encontrar o volume do problema.
Passo 2
Mas antes vamos escolher um elemento de volume, para assim podermos integrar, com isso:
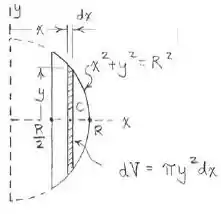
Pronto! Escolhido o elemento de volume vamos integrar ele em relação a x e temos o nosso volume.
Agora precisamos deixar em função de x para podermos integrar, o problema já nos informa que é uma região circular, ou seja, a função que descreve a curva é:
Sendo que, se olharmos o problema de frente vemos que o raio é a coordenada y e tem uma profundidade x. Assim:
Passo 3
Tendo a função que descreve o nosso problema fica mais fácil de integra, atente que a região de integração está entre . Dessa maneira:
Agora basta resolvermos essa integral que teremos nosso volume, sendo que:
Passo 4
Ante de aplicar a equação para achar o centroide na coordenada x, vamos resolver a integral:
Depois é só dividir pelo volume que teremos o ponto. Com isso,
Logo,
Pronto! Só substituir na equação, se tiver alguma dificuldade na resolução das integrais recomendo que revise o assunto de integrais em cálculo que encontra na própria plataforma. Agora vamos substituir: