Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas fundamentais - Ex. 03
Se a barra OA de massa desprezível é submetida ao momento de binário M = 9 N.m, determine a velocidade angular da engrenagem interior de 10 kg para t = 5 s após ela partir do repouso. A engrenagem tem um raio de giração em relação a seu centro de massa , e ela rola sobre a engrenagem exterior fixa. O movimento ocorre no plano horizontal.
Passo 1
Começaremos o exercício escrevendo a velocidade linear da engrenagem interior em função da velocidade angular da mesma:
Passo 2
Agora iremos aplicar o somatório de momento para a engrenagem interior com relação ao ponto O com o auxílio do diagrama a seguir para descobrir o valor da reação tangencial:
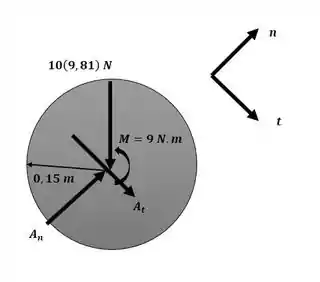
Passo 3
Agora iremos aplicar o princípio do impulso e da quantidade de movimento angular para os instantes final e inicial:
Resposta
Exercícios de Livros Relacionados
O volante de 100 kg tem um raio de giração em relação a seu centro de gravidade O de k O = 0,225m , Se ele gira no sentido anti-horário com uma velocidade angular de 1200 rev/min antes de o freio ser
O volante A de 15 kg tem um raio de giração em relação a seu centro de 100 mm. O disco B tem uma massa de 25 kg e está acoplado ao volante através de uma correia que não desliza em suas superfícies de
O corpo rígido (placa) tem uma massa m e gira com uma velocidade angular ω em relação a um eixo passando pelo ponto fixo O. Demonstre que os momentos de todas as partículas compondo o corpo podem ser
O volante A tem uma massa de 30 kg e um raio de giração k C = 95m m . O disco B tem uma massa de 25 kg, está preso com pino em D, e está acoplado ao volante usando uma correia que está submetida a uma
O disco circular de 25 kg está fixado ao garfo através de um eixo liso A. O parafuso C é usado para travar o disco ao garfo. Se o garfo é submetido a um torque M = 5 t 2N . m , onde t é dado em segund