Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 24
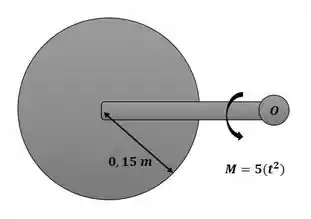
O disco circular de 25 kg está fixado ao garfo através de um eixo liso A. O parafuso C é usado para travar o disco ao garfo. Se o garfo é submetido a um torque , onde t é dado em segundos e o disco está travado, determine a velocidade angular do garfo quando t = 3 s, partindo do repouso. Despreze a massa do garfo.
Passo 1
Começaremos o exercício calculando o momento de inércia do disco ao redor do seu centro de massa:
Passo 2
Como o garfo rotaciona ao redor de um ponto fixo:
Passo 3
Agora podemos aplicar o princípio do momento angular em torno do ponto O com o auxílio do esquema a seguir:
Resposta
Exercícios de Livros Relacionados
Uma lata de suco congelado está apoiada sobre a prateleira horizontal de uma porta de congelador conforme mostrado. Com que velocidade angular máxima Ω a porta pode ser ‘batida’ contra sua vedação e n
As duas barras esbeltas, cada uma com uma massa de 4 kg, são articuladas em B e C . Se um impulso horizontal ∫ F d t = 14N ∙ s é aplicado à extremidade A da barra inferior, por um intervalo de 0,1 s,
234. O sistema do problema 6.23 é representado aqui. O carrinho B se desloca para a direita com aceleração a = 2 g . Se m = 0,5k g , l = 0,6m e k = 75N ⋅ m / r a d , determine o deslocamento angular e
O pendulo de 8 kg com centro de massa em G e um raio de giração de 235 mm em relação a O é liberado a partir do repouso na posição horizontal θ = 0 ° .Represente graficamente a componete n da força su
O centro de massa G da pessoa de 70 kg mostrada tem uma velocidade máxima de 4 m/s na posição mais baixa do balanço. Para as dimensões dadas, calcule o momento fletor M suportado pelas vértebras lomba