Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 215
Determine o momento fletor máximo, , para a viga carregada e especifique a distância à direita da extremidade onde ocorre.
Passo 1
Devemos perceber primeiro que na parte direita da viga, depois de B, teremos uma força cortante que é negativa, como mostra a figura:
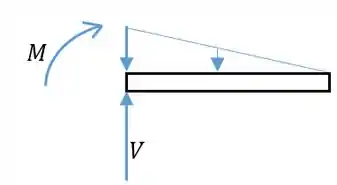
Sabemos que:
Então se é negativo, é decrescente nessa parte da viga. Logo, o máximo de deve ocorrer na parte esquerda da viga, e não precisamos nos preocupar com a parte depois de . Vamos obter a partir da integração de com os valores de variando de a m, da seguinte forma:
Pois .
Passo 2
Primeiro calculamos a resultante da distribuição de forças na viga e o ponto no qual ela é aplicada. A resultante é a área abaixo da distribuição de forças:
A força resultante será aplicada no centroide da área da região triangular. Sabemos que o centroide de um triângulo fica a uma distância de de sua base, sendo a altura relativa a essa base. Se a base for a linha vertical com comprimento de 600, a altura tem 3 m e então o centóide fica a 1 m de . Agora fazendo o momento em torno de , achamos a força em :
Então, pelo equilíbrio em :
Passo 3
Vamos então calcular . Isolamos uma parte da viga, fazendo um corte entre e de tamanho :
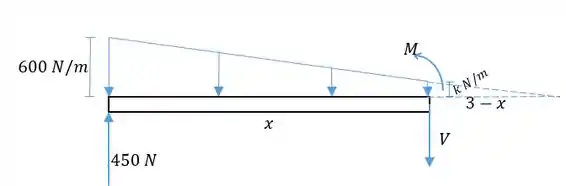
Pela imagem, vemos que agem nessa parte da viga a distribuição de forças, a força em e o cortante . A resultante da distribuição de forças é calculada pela área do diagrama de forças até . Pela semelhança de triângulos na figura:
É o valor densidade linear de carga a metros de . Então, pela fórmula da área do trapézio:
Agora fazendo o equilíbrio em encontramos para :
Passo 4
Então já temos nossa função para a parte que queremos. Vamos obter integrando . Para :
Teremos um máximo de quando , ou seja, quando , então:
Dividindo tudo por 50:
Vamos agora resolver essa equação dos egundo grau:
Como queremos um valor menor que 2:
E o valor de nesse ponto é: