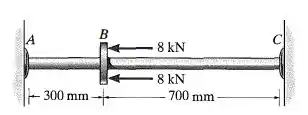
O tubo de aço A-36 tem raio externo de e raio interno de . Se ele se ajustar exatamente entre as paredes fixas antes de ser carregado, determine a reação nas paredes quando for submetido à carga mostrada.
Passo 1
Fala aí pessoal, partiu resolver mais um exercício de resmat. Primeiro, vamos esboçar o DCL (diagrama de corpo livre):
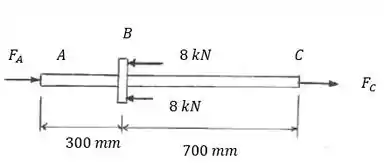
Como a carga é aplicada para a esquerda, a gente vai supor as reações no sentido contrário, tá bem?
Passo 2
Agora, vamos utilizar a equação de equilíbrio para o eixo , partiu fazer o somatório das forças em X ;)
Temos duas variáveis e uma equação. Precisamos achar mais uma, para ter informações suficientes para ter a solução, ok?
Passo 3
Pensa comigo. Temos uma barra do lado da outra. E elas duas estão entre dois apoios. Logo, o comprimento entre esses dois apoios não muda. Certo?
A barra da esquerda vai sofrer compressão . E a da direita vai sofrer uma tração . Como no total precisa continuar do mesmo tamanho, tem alongamento , então a soma dos dois alongamentos dos dois segmentos precisam ser
Aí a gente pode usar a expressão para alongamento dos dois lados, considerando que ambos os tubos tem o mesmo material e mesma seção transversal.
Passo 4
E se olharmos a nossa figura, vemos que as cargas axiais que geram esse deslocamento (o esfoço interno normal) para o tubo pode ser dada pela reação na parede e para o tubo pode ser dada pela reação na parede ...
Assim, pelas relações carga-deslocamento, temos que:
Com isso, temos um sistema de duas equações e duas incógnitas. Resolvendo ele, podemos encontrar e , temos:
Achamos mais uma equação!
Passo 5
Resolvendo esse sistema, temos que as reações nas paredes em e em , são:
Agora podemos achar FA.