Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 45

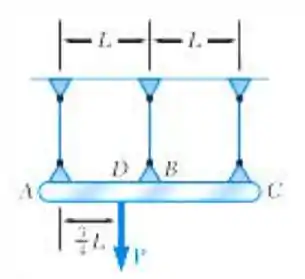
A barra rígida ABC é suspensa por três cabos de mesmo material. A área da seção transversal do cabo B é igual à metade da área das seções transversais dos cabos em A e C. Determine a tração em cada um dos cabos causada pela carga P mostrada.

Passo 1

Fala aí gurizada tudo belezinha?????? Antes de determinarmos a tensão e o deslocamento pedidos pelo exercício, vamos então desenhar o diagrama corpo livre, vem comigo :D

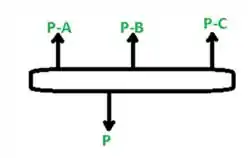
Vamos agora gurizada calcular o somatório do momento em A, vem comigo :D

    + ∑ M A = F   x   d = 0

2 L P C + L P B - 3 4 L P = 0

      P C = 3 8 P - 1 2 P B

E agora o momento em C, partiu !!

+ ∑ M C = 0 :       2 L P A - L P B - 5 4 L P = 0

P A = 5 8 P - 1 2 P A

Seja L o comprimento dos fios A, B, C temos respctivamente:

δ A = P A l E A = l E A 5 8 P - 1 2 P B δ B = P B l E A 2 = 2 l E A P B δ C = P C l E A = l E A ( 3 8 P - 1 2 P B )    

Passo 2

A partir do diagrama de corpo livre abaixo podemos considerar a deformação.

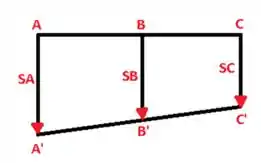
  δ A - δ B = δ B - δ C ou, δ B = 1 2 δ A + δ C                                                                                                  

Substituindo nas equações obtidas no passo 1 temos:

  l E A 2   P B = 1 2 l E A 5 8 P - 1 2 P B + 3 8 P - 1 2 P B - 1 2 P B                                                         5 2 P B = 1 2 P ;     P B = 1 5 P

Assim temos as seguintes forças de tração:

P A = 5 8 P - 1 2 P 5 = 21 40 P P C = 3 8 P - 1 2 P 5 = 11 40 P

Sendo: P A + P B + P C - 1,000 P = 0

21 40 P + P B + 11 40 P - 1,000 P = 0

P B = 0,2   P

Resposta

  1. P B = 0,200 P
  2. P A = 0,515 P
  3. P C = 0,275 P
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que existe um espaçamento de 0,508 mm quando a temperatura é de 23,9°C, determine (a) a temperatura na qual a tensão normal na barra de alumínio será igual a -75,8 MPa e (b) o comprimento exat
Uma barra formada por duas partes cilíndricas AB e BC está impedida de se deslocar em ambas as extremidades. A parte AB é feita de aço ( E a ç o = 200G P a , a a ç o = 11,7x10 - 6 / ° C ) ç ç e a part
Duas barras de aço ( E a ç o = 200G P a e a a ç o = 11,7x10 - 6 / ° C ) ç ç são utilizadas para reforçar uma barra de latão ( E l a t ã o = 105G P a ,a l a t ã o = 20,9x10 - 6 / ° C ) ã ã que está sub
a barra de aço ABC está rigidamente conectada aos suportes e livre de tensões à temperatura de 25°C. O aço é considerado elastoplástico, com E = 200G P aeσ E = 250M P a . A temperatura de ambas as par
Uma barra de aço uniforme de seção transversal com área A é ligada a suportes rígidos e está livre de tensões a uma temperatura de 7,22°C. O aço é considerado elastoplástico com σ E = 248M P aeE = 200