Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 42

Resolva o Problema 2.41 supondo que a barra AC é feita de latão e a barra CE é feita de aço.

Passo 1

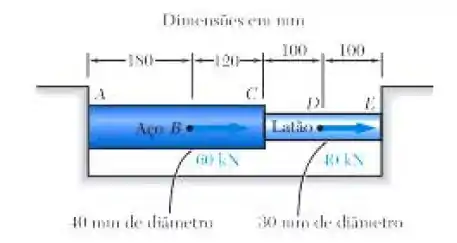
E ai gurizada tudo belezinha??? Espero que sim!!! Para encontrarmos as reações pedidas no enunciado é necessário que a gente faça nosso famoso diagrama de corpo livre, vem comigo :D

Observem que este elemento possui 2 componentes de áreas diferentes, então temos que calcular a área para cada uma, vem comigo :D

A para C, considerando o módulo de elasticidade de : E = 105   x   10 9 P a A = π 4 40 2 = 1,25664   x   10 3 m m 2 = 1,25664   x   10 - 3 m 2

Assim se multiplicarmos a área pelo modulo temos: E A = 131,947   x   10 6 N

De maneira análoga para a seção CE

C para E: E = 200   x   10 9 P a A = π 4 30 2 = 706,86   m m 2 = 706,86   x   10 - 6 m 2 E A = 141,372   x   10 6 N

Então para determinar a reação vamos ter que utilizar a equação do alongamento, vamos relembrar os dados fornecidos pelo enunciado :D

L = 180 m m = 0,180 m

A para B: P = R A δ A B = P L E A = R A   x   0,180 131,947   x   10 6 = 1,36418   x   10 - 9 R A

B para C: P = R A - 60   x   10 3 L = 120 m m = 0,120 m δ B C = P L E A = ( R A - 60   x   10 3 )   x   0,120 131,947   x   10 6 = 909,456   x   10 - 12 R A - 54,567   x   10 - 6

C para D: : P = R A - 60   x   10 3 L = 100 m m = 0,100 m δ B C = P L E A = ( R A - 60   x   10 3 )   x   0,100 141,372   x   10 6 = 707,354   x   10 - 12 R A - 42,441     x   10 - 6

Calmem que falta pouco, analogamente temos que fazer para o restante do comprimento do elemento, vejam no passo abaixo :D

Passo 2

D para E: P = R A - 100   x   10 3 L = 100 m m = 0,100 m δ D E = P L E A = ( R A - 100   x   10 3 )   x   0,100 141,372   x   10 6 = 707,354   x   10 - 12 R A - 70,735   x   10 - 6

A para E: δ A E = δ A B + δ B C   + δ C D + δ D E   = 3,68834   x   10 - 9 R A - 167,743   x   10 - 6

Como o ponto E não pode se mover em relação a A,

δ A E = 0

Agora sim podemos definir as reações e o alongamento ,vem comigo ta quase no fim !!

  1. = 3,85837   x   10 - 9   R A - 167,743   x   10 - 6 = 0     R A = 45,479   x   10 3 N   R E = R A -   100   x   10 3 = 45,479   x   10 3 - 100   x   10 3   = - 54,521   x   10 3  

  2. δ C + δ A B   + δ B C = 2,27364   x   10 - 9 R A - 54,567   x   10 - 6   = 2,27364   x   10 - 9   x   45,479   x   10 3 - 54,567   x   10 - 6 = 48,8   x   10 - 6 m

Resposta

  1. R A = 45,5   k N ← R E = 54,5   k N ←

  2. δ C = 48,8   μ m →
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra de latão amarelo quadrada não deve se alongar mais de 1,4 mm quando submetida a uma força de tração. Sabendo que E = 70G P a e que a resistência à tração admissível é120 MPa, determine (a) o
A barra BD feita de aço (E = 200G P a ) é utilizada para contenção lateral da haste comprimida ABC. O máximo esforço que se desenvolve em BD é igual a 0,02P. Se a tensão não deve exceder 124,1 MPa e a
O cabo BC de 4 mm de diâmetro é feito de um aço com E = 200G P a . Sabendo que a máxima tensão no cabo não pode exceder 190 MPa e que a deformação do cabo não deve exceder 6 mm, determine a máxima for
Um tubo de alumínio com 250 mm de comprimento (E = 70G P a ) , 36 mm de diâmetro externo de 28 mm de diâmetro interno pode ser fechado em ambas as extremidades por meio de tampas com rosca simples de
Ambas as partes da barra ABC são feitas de um alumínio para o qual E = 70G P a . Sabendo que a intensidade de P é 4 kN, determine (a) o valor de Q e modo que o deslocamento em A seja zero e (b) o desl