Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 100

A barra tem área de seção transversal de 300   mm 2 e é feita de um material cujo diagrama tensão-deformação pode ser aproximado pelos dois segmentos da reta mostrados na figura. Determine o alongamento da barra resultante do carregamento aplicado.

Passo 1

Uma barra presa a um pino em A é esticada por duas forças de tração: 40   kN em B e 15   kN em C .

A questão nos dá um gráfico para a relação tensão deformação.

Primeiro, a tensão cresce de forma linear até σ 1 = 140   MPa em ϵ 1 = 0,001 . Em seguida, ainda temos uma relação linear, mas a inclinação muda, indo até σ 2 = 280   MPa em ϵ 2 = 0,021 .

Além disso, sabemos que a barra tem as seguintes características:

  • Área transversal: A = 300   mm 2 .
  • Comprimento inicial A B : L A B = 1,5   m .
  • Comprimento inicial B C : L B C = 0,6   m .

Queremos saber o alongamento δ que a barra sofre por causa dos carregamentos! Esse δ será a soma dos alongamentos dos segmentos A B e B C :

δ = δ A B + δ B C

Por causa do gráfico, se acharmos as tensões σ podemos calcular as deformações ϵ para cada parte da barra.

E aí é só usarmos a relação entre deformação ϵ , comprimento inicial L e alongamento δ :

ϵ = δ L

Beleza! Temos um plano. Primeiro precisamos das tensões.

Passo 2

Vamos começar entendendo que força age em cada seção. Lembrando do equilíbrio de forças, veja a figura.

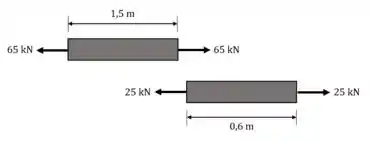
Seções à esquerda do ponto B estão sendo tracionadas por F A B = 65   kN , e à direita por F B C = 25   kN .

Vamos ver as tensões desenvolvidas em cada parte:

σ = F A

σ A B = 65   kN 300   mm 2 = 216,667   MPa

σ B C = 25   kN 300   mm 2 = 83,334   MPa

Passo 3

Agora, vamos ver cada caso. Temos que σ B C < σ 1 , então a deformação ϵ B C no segmento B C ocorre de acordo com a primeira parte do gráfico!

Use a relação linear do gráfico (regra de três) para achar ϵ B C :

ϵ B C σ B C = ϵ 1 σ 1

ϵ B C 83,334   MPa = 0,001 140   MPa

ϵ B C = 0,000595

Agora veja o alongamento da seção B C :

ϵ B C = δ B C L B C           →           0,000595 = δ B C 0,6   m

δ B C = 0,357   mm

Passo 4

Boa! Pro segmento A B vai ser quase a mesma coisa. Temos que σ A B > σ 1 , então a deformação ϵ B C no segmento B C ocorre de acordo a segunda parte do gráfico.

Use a relação linear do gráfico (regra de três) para achar ϵ A B . Cuidado, a reta da segunda parte começa a partir de σ 1 = 140   MPa em ϵ 1 = 0,001 !

ϵ A B - ϵ 1 σ A B - σ 1 = ϵ 2 - ϵ 1 σ 2 - σ 1

ϵ A B - 0,001 216,667   MPa - 140   MPa = 0,021 - 0,001 280   MPa - 140   MPa

ϵ A B = 0,011952

Agora veja o alongamento do segmento A B :

ϵ A B = δ A B L A B           →           0,011952 = δ B C 1,5   m

δ B C = 17,928   mm

Passo 5

Só falta somar:

δ = δ A B + δ B C

δ = 18,28   mm

Resposta

Alongamento: δ = 18,28   mm .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O diagrama tensão-deformação de um material pode ser descrito pela curva σ = c ϵ 1 / 2 . Determine a deflexão δ da extremidade de uma haste feita desse material se ela tiver comprimento L , área de se
A barra rígida é sustentada por um pino em A e dois cabos de aço, cada um com diâmetro de 4mm . Se a tensão de escoamento para os cabos for σ e = 530MPa e E a ç o = 200GPa ç , determine a intensidade
A barra tem área de seção transversal de 625mm 2 . Se uma força P = 225kN for aplicada em B e, então, removida, determine a tensão residual nas seções A B e B C . σ e = 210MPa .
A barra rígida é sustentada por um pino em A e dois cabos de aço, cada um com diâmetro de 4mm . Se a tensão de escoamento para os cabos for σ e = 530MPa e E a ç o = 200GPa ç , determine ( a ) a intens
Determine o alongamento da barra no Problema 4.108 quando são removidos tanto a carga P quanto os apoios.