Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas - Ex. 32
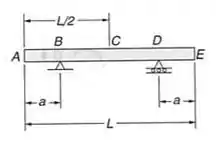
Uma barra uniforme está apoiada em dois pontos e . Determine a distância a das extremidades da barra até os apoios, para que as deflexões em sejam iguais e para baixo.
Passo 1
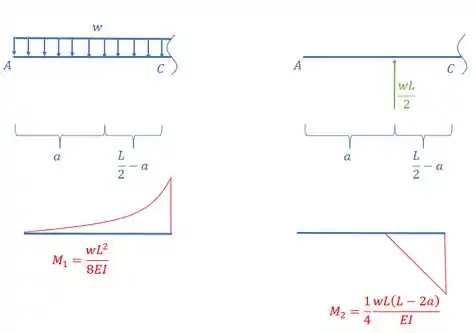
E ai galera, até agora resolvemos apenas problemas com engastes, mas agora iremos começar a resolver problemas biapoiados, os conceitos vão se manter iguais aos que já conhecíamos, mas agora vamos ter que tomar um cuidado importante com o nosso diagrama de momentos fletores, então é de suma importância que fiquemos atento a ele, e por isso, vamos começar por ele, calculando primeiro a reação de apoio da nossa viga.
E para isso consideramos uma carga distribuída por toda a viga, assim podemos considerar uma carga distribuída sobre a viga.
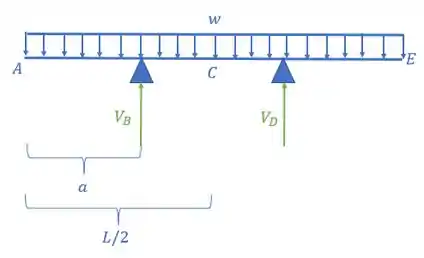
E por fim tem uma coisa bem legal de se notar, a nossa viga é simétrica com cargas simétricas, certo? Então não precisamos desenhar o diagrama inteiro da viga, podemos desenhar só metade do nosso diagrama, e analisando o que temos até aqui, vamos ver que é exatamente isso aqui:
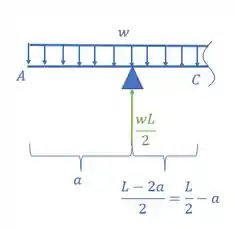
Assim o nosso diagrama de momentos fletores calculando um diagrama para cada carregamento será dado por:
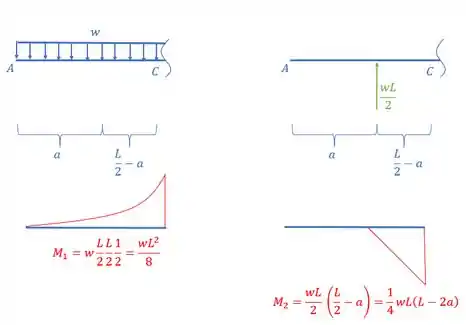
E por fim, temos que dividir o nosso diagrama pelo nosso , assim, teremos que:
Passo 2
Sabemos que a deformação relativa entre pontos é dada por:
Porém o enunciado deixa claro que os pontos A e C estão deformando na vertical do mesmo valor, ou seja, a deformação relativa tem que ser zero, assim, teremos que:
Agora basta determinarmos a área e a distância de cada área até a nossa extremidade, assim, temos que:
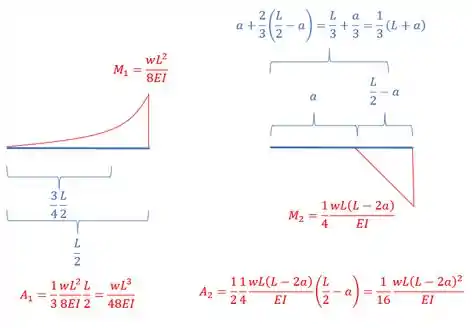
Aqui podemos fazer uma mudança legal para os nossos cálculos, e basicamente são duas, podemos simplificar tudo dividindo os dois termos da equação por:
Assim temos que:
E podemos fazer a seguinte relação, considerando:
Assim temos que:
Resolvendo a nossa equação, obtemos que:
Sabemos que a aqui temos que analisar duas coisas, primeiro, o nosso U é uma razão de comprimentos, logo, queremos a solução positiva, e também queremos a distancia mínima que causa o que o enunciado pede, ou seja, também descartamos o maior valor, assim, temos que:
Mas sabemos que:
Assim, a nossa distância mínima vai ser dada por: