Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 3.Problemas - Ex. 46
Determine a massa máxima da caixa para que a tração desenvolvida em qualquer cabo não ultrapasse 3 kN.
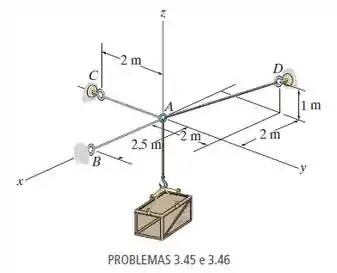
Fonte: Estática Mecânica para Engenharia – 14ª ed
Passo 1
Fala aí, bora pra mais uma?!
Partiu!!
Bem, o problema quer que o sistema esteja em equilíbrio, e é muito parecido com o problema 3.45, então vamos fazer assim:
- Encontrar as componentes das forças em cada coordenada;
- Realizar o somatório de forças e igualar a zero, para o equilíbrio.
A força de tração exercida em D pode ser encontrada por:
A força de tração em C:
E a força de tração em B:
E a força peso da caixa é:
Passo 2
Agora vamos ao somatório de forças em relação a z:
Como o valor máximo que pode receber é 3kN, então podemos encontrar o peso da caixa por:
P.s: esse valor é encontrado utilizando os valores sem aproximação:
Assim, a massa da caixa é:
Resposta
Portanto:
Exercícios de Livros Relacionados
As extremidades dos três cabos estão presas a um anel em A e à borda de uma placa uniforme de 150k g . Determine a tração em cada um desses cabos para o equilíbrio.
Se cada cabo pode suportar uma tração máxima de 1000N , determine a maior massa que o cilindro pode ter para o equilíbrio.
Determine a tração desenvolvida nos cabos AB, AC e AD cabos para o equilíbrio do cilindro de 75k g .
As extremidades dos três cabos estão presas a um anel em A e à borda da placa uniforme. Determine a maior massa que a placa pode ter se cada cabo pode suportar uma tração máxima de 15k N .
O vaso de 50k g é sustentado por A, pelos três cabos. Determine a força que atua em cada cabo para o equilíbrio. Considere d = 2,5 m .