Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 129

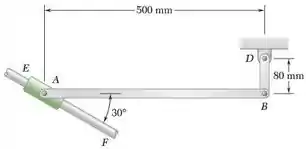
A barra uniforme BD de 3 kg é ligada à manivela BD e ao colar de peso desprezível, que pode deslizar livremente ao longo de uma barra EF. Sabendo que, na posição mostrada na figura, a manivela BD gira com uma velocidade angular de 15 rad /s e uma aceleração angular de 60 rad /s2, ambas no sentido horário, determina a reação em A.

Passo 1

Manivela BD:

ω B D = 15   r a d / s ,             v B = 0.08   m 15   r a d / s = 1.2   m / s ←

α B D = 60   r a d / s 2

a B x = 0.08   m 60   r a d / s 2 = 4.8   m / s 2 ←

a B y = 0.08   m 15   r a d / s 2 = 18   m / s 2 ↑

Passo 2

Haste AB:

Velocidade: Centro instantâneo em C:

C B = 0.5   m / t a n t a n   30 ° = 0.86603   m  

ω A B = v B C B = 1.2   m / s 0.86603   m = 1.3856   r a d / s  

Passo 3

Aceleração:

a A / B t = A B α A B = 0.5 α A B ↓

a A / B n = A B ω A B 2 = 0.5 1.3856 2 = 0.96   m / s 2 →

a A / B t = G B α A B = 0.25 α A B ↓

a A / B n = G B ω A B 2 = 0.25 1.3856 2 = 0.40   m / s 2 →

a A = a B + a B / A = a B + a B / A t + a G / A n

a A     30 ° = 4.8 ← + 18 ↑ + 0.5 α A B ↓ + 0.96 →

  + ← a A c o s c o s   30 ° = 4.8 - 0.96 ;               α A = 4.434   m / s 2         30 °

+ ↑ 4.434 s i n s i n   30 ° = 18 - 0.5 α A B ;               α A B = 31.566   r a d / s 2    

a _ = a B + a G / B = a B + a G / B t + a G / B n

a _ = 4.8 → + 18 ↑ + 0.25 32.566 ↓ + 0.48 →

  + ← a _ x = 4.8 - 0.48 = 4.32 ;               a _ x = 4.32   m / s 2   ←  

+ ↑ a y = 18 - 2.892 = 10.108 ;                 a y = 10.108   m / s 2 ↑

Passo 4

Cinética:

I _ = 1 12 m A B 2 = 3   k g 12 0.5   m 2 = 0.0625   k g ∙ m 2

I _ = 1 12 m A B 2 = 3   k g 12 0.5   m 2 = 0

+ Σ M B = Σ M B e f f :             A s i n s i n   60 °   0.5   m - m g 0.25   m = - I _ a A B + m a _ B 0.25   m

0.433   A - 3   k g 9.81   m / s 2 0.25   m = - 0.0625   k g ∙ m 2 31.566   r a d / s 2

+ 3   k g 10.108   m / s 2 0.25   m

0.433   A - 7.358 = - 1.973 + 7.581

A = 29.94   N

Resposta

A = 29.9   N     60 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9. Determine a velocidade angular da bobina. O cabo se enrola em torno do núcleo interno e a bobina não desliza na plataforma P.
7. Se o rolete A se desloca para a direita com uma velocidade constante v A = 3m / s , determine a velocidade angular da barra de ligação e a velocidade do rolete B no instante θ = 30 ° .
34. Se o eixo e a placa giram com uma velocidade angular constante ω = 14 r a d s , determine a velocidade e aceleração no ponto C localizado no canto da placa no instante mostrado. Expresse o resulta
40. O disco A rola sem deslizar sobre a superfície do cilindro fixo B. Determine a velocidade angular de A se seu centro C tem uma velocidade v C = 5 m s . Quantas revoluções A realizará em torno de s
33. Se a barra parte do repouso na posição mostrada e um motor a aciona por um curto período com uma aceleração angular a = 1,5 e t r a d s 2 , onde t é dado em segundos, determine a intensidade da ve