Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 40

40. O disco A rola sem deslizar sobre a superfície do cilindro fixo B. Determine a velocidade angular de A se seu centro C tem uma velocidade v C = 5 m s . Quantas revoluções A realizará em torno de seu centro logo após a barra de ligação DC completar uma revolução?

Passo 1

Para resolver está questão basta utilizar as equações e raciocínios desenvolvidos ao longo dessa seção inicial do capitulo 16. Seria importante também antes de começar a resolver as questões problemas, fazer as 6 questoes fundamentais pois de alguma forma a resolução delas ajudará em praticamente todas as resoluções. Pois, cada questão problema estará relacionada com algum conceito de alguma questão fundamental.

Passo 2

Um esboço do que foi dito no enunciado pode ser representado por:

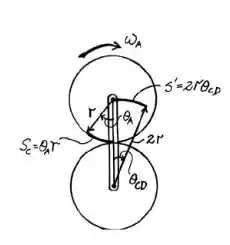
Passo 3

A partir daí, temos que a distância percorrida pela roda A será dada por:

s = θ A . r

d s d t = r . d θ A d t

5 = ω A . 0,15

ω A = 33,3   r a d / s

Passo 4

Pelo esboço, temos que:

s ´ = 2 r θ C D = s = θ A r

2 θ C D = θ A

Logo, A realizará duas revoluções em torno do seu centro.

Resposta

ω A = 33,3   r a d / s

Logo, A realizará duas revoluções em torno do seu centro.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco uniforme de 5 kg está ligado a uma haste uniforme BC de 3 kg por meio de um pino AB sem atrito. Uma corda elástica é enrolada em torno da borda do disco e é ligada a um anel em E. Tanto o ane
Uma roda de raio r e raio de giração em torno do centro de massa é liberada a partir do repouso no declive e rola sem deslizar. Deduza uma expressão para aceleração do centro da roda em termos de r, k
Um volante de motor de raio de giração em torno do centro de massa k é preso rigidamente a um eixo que pode rolar ao longo de trilhos paralelos. Representando por μ S o coeficiente de atrito estático
Uma esfera homogênea S, um cilindro uniforme C e um tubo fino P estão em contato quando são liberados a partir do repouso no declive mostrado na figura. Sabendo que todos os três objetos rolam sem des
Deduza a equação Σ M C = I C a para o disco e rolamento da Fig. 16.17, onde Σ M C Representa a soma dos momentos das forças externas em relação ao centro instantâneo C, e IC é o momento de inércia do