Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas fundamentais - Ex. 9
9. Determine a velocidade angular da bobina. O cabo se enrola em torno do núcleo interno e a bobina não desliza na plataforma P.
Passo 1
O diagrama esquemático do carretel e da plataforma que nos ajudará na resolução do problema pode ser representado por:
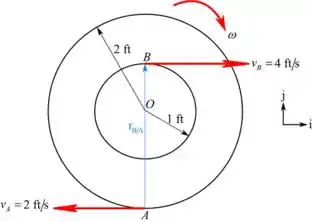
Uma vez que o carretel não desliza na plataforma. O ponto A tem a mesma velocidade que a plataforma.
O vetor de posição direcionado de A para B é expresso como,
Calcule a velocidade angular usando a equação de velocidade,
Equacionando o coeficiente,
Portanto, a velocidade angular do carretel é
Show, conseguimos termina!!
Resposta
Exercícios de Livros Relacionados
Sabendo que no instante mostrado na figura a velocidade angular da barra BE é de 4r a d/ s no sentido anti-horário, determine (a) a velocidade angular da barra AD, (b) a velocidade do colar D, (c) a v
Sabendo que no instante mostrado na figura a velocidade do colar D é de 1,6m / s para cima, determine (a) a velocidade angular da barra AD, (b) a velocidade do ponto B, (c) a velocidade do ponto A.
A barra AB desliza livremente ao longo do chão e no plano inclinado. Deduza por v A a velocidade do ponto A , obtenha uma expressão para (a) velocidade angular da barra, (b) a velocidade da extremidad
A barra AB desliza livremente ao longo do chão e no plano inclinado. Sabendo que θ = 20 ° , β = 50 ° , l = 0,6m , v A = 3m / s , determine (a) velocidade angular da barra, (b) a velocidade da extremid
O braço ABD está conectado por pinos ao colar em B e à manivela DE. Sabendo que a velocidade do colar B é de 400m m / s para cima, determine (a) a velocidade angular do braço ABD e (b) a velocidade do