Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 37

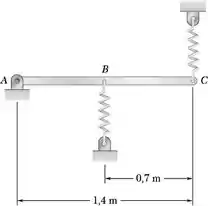
A barra uniforme AC de 5 kg está presa a molas com constantes k = 500 N/m em B e k = 620 N/m em C, que podem atuar em tração ou compressão. Se a extremidade C for ligeiramente abaixada e liberada, determine (a) a frequência de vibração, (b) a amplitude do movimento do ponto C, sabendo que a velocidade máxima desse ponto é de 0,9 m/s.

Passo 1

O enunciado pede que a gente encontre (a) a frequência de vibração, (b) a amplitude do movimento do ponto C, sabendo que a velocidade máxima desse ponto é de 0,9 m/s.

F B = k B x B + δ S T B = k B 0.7 θ + δ S T B

F C = k C x C + δ S T C = k C 1.4 θ + δ S T C

Passo 2

Equação de movimento.

+ Σ M A = Ε M A eff :

0.7 k B 0.7 θ + δ S T B - m g + 1.4 k C 1.4 θ + δ S T C = - I - α - 0.7 m a t

Mas em equilíbrio θ = 0 ,

Σ M A = 0 = 0.7 k B δ S T B - m g + 1.4 k C δ S T C

Substituindo a Equação (2) pela Equação (1),

I - α + 0.7 m a t + 0.7 2 k B θ + 1.4 2 k C θ = 0

Passo 3

Cinemática α = θ ¨

a t = 0.7 α = 0.7 θ ¨

I - + m 0.7 2 θ ¨ + 0.7 2 k B + 1.4 2 k C θ = 0

I - = 1 12 m l 2 = 1 12 5   kg 1.4   m 2 = 0.8167   kg ∙ m 2

. 7 2 m = 0.49   m 2 5   kg = 2.45   kg ∙ m 2

0.7 2 k B + 1.4 2 k C = 0.49   m 2 500   N/m + 1.96   m 2 620   N/m = 245 + 1215.2 = 1460.2   N ∙ m

0.8167 + 2.45 θ ¨ + 1460.2 θ = 0

θ ¨ + 1460.2   N ∙ m 3.267   kg ∙ m 2 θ = 0

θ ¨ + 447 θ = 0                 N/kg   ∙ m = s -2

Passo 4

  1. Frequência natural.

    2. ω n = 447  s -2 = 21.14   rad/s

    Passo 5

  2. Velocidade máxima.

θ = θ m sin ⁡ ω n t + ϕ

θ ˙ = θ m ω n cos ⁡ ω n t + ϕ

Velocidade máxima angular.

θ ˙ m = θ m ω n

Velocidade máxima em C.

x ˙ C m = 1.4 θ ˙ m = 1.4   m θ m ω n

θ m = 0.9   m/s 1.4   m 21.14   rad/s = 0.03041   rad

Passo 5

Amplitude máxima em C.

x C m = 1.4   m θ m = 1.4   m 0.03041

x C m = 0.0426   m

Resposta

a )   f n = ω n 2 π = 21.14 2 π = 3.36   Hz

b )   x C m = 42.6   mm

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a velocidade máxima e a aceleração máxima de uma partícula que se move em movimento harmônico simples com uma amplitude de 5 mm e um período de 0,1 s.
Uma caixa de instrumento A está aparafusada numa mesa vibratória como mostrado na figura. A mesa se movimenta verticalmente em movimento harmônico simples na mesma frequência do motor de rotação variá
Um bloco de 15 kg é suportado pela mola como mostrado na figura. Se o bloco é movido verticalmente para baixo até sua posição de equilíbrio e liberado, determine (a) o período e a frequência do movime
Um bloco de 5 kg preso à extremidade inferior de uma mola cuja extremidade superior é fixa vibra com um período de 6,8 s. Sabendo que a constante k da mola é inversamente proporcional ao seu comprimen
Um pacote de instrumento B é colocado na mesa C como mostrado na figura. A mesa foi projetada para se deslocar horizontalmente em movimento harmônico simples com uma frequência de 3 Hz. Sabendo que o