Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 52
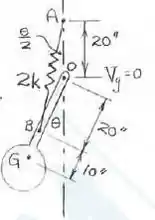
A seção transversal de um alçapão articulado em A e tendo uma massa me um centro de massa em G é mostrado na figura. A mola é comprimida pela haste que é fixada na extremidade inferior da porta e que passa pelo bloco giratório em B. Quando θ = 0, a mola não está deformada. Mostre que com a rigidez apropriada k da mola, a porta estará em equilíbrio para qualquer ângulo θ.
Passo 1
O enunciado pede que a gente Mostre que com a rigidez apropriada k da mola, a porta estará em equilíbrio para qualquer ângulo θ.
Comprimento AB
Passo 2
Resposta
Exercícios de Livros Relacionados
Para o mecanismo mostrado, a mola de rigidez k tem um comprimento não alongado de essencialmente zero, e o elo maior tem uma massa m com centro de massa em B. A massa do elo menor é desprezível. Deter
Duas barras idênticas são soldadas em um ângulo de 120∘ e articuladas em O conforme mostrado. A massa da aba de suporte é pequena em comparação com a massa das barras. Investigue a estabilidade da pos
A alça é presa a uma das engrenagens conectadas por mola, que são montadas em rolamentos fixos. A mola de rigidez k conecta dois pinos montados nas faces das engrenagens. Quando a alça está na posição
A figura mostra a vista lateral OA de uma porta de ventilador uniforme de massa m que fecha a abertura OC em uma parede vertical. A mola de rigidez k é descomprimida quando θ = 0, e a haste de luz que
Um dos requisitos críticos no projeto de uma perna artificial para um amputado é evitar que a articulação do joelho dobre sob a carga quando a perna está esticada. Como uma primeira aproximação, simul