Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 38

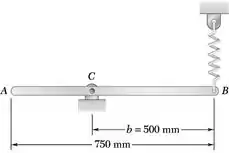
A barra uniforme mostrada na figura tem uma massa de 7,5 kg e está presa a uma mola de constante k = 800 N/m. Se a extremidade B da barra é abaixada 10 mm e liberada, determine (a) o período de vibração, (b) a máxima velocidade da extremidade B.

Passo 1

O exercício pede que a gente encontre (a) o período de vibração, (b) a máxima velocidade da extremidade B.

k = 4   lb/in. = 48   lb/ft

W = 15   lb

onde

F = k x + δ ST = k 1.5 θ + δ ST

m a - = m r - α = 15 g 0.25   ft θ ¨ = 3.75 g θ ¨

I - α = 1 12 15 g 2.5   ft 2 θ ¨ = 7.8125 g θ ¨

Passo 2

  1. + Σ M C = Ε M C eff :                 W 0.25   ft - F 1.5   ft = I - α + m a - 0.25   ft

    W = 0.25 - k 1.5 θ + δ ST 1.5   ft = 7.8125 g θ ¨ + 3.75 g θ ¨ 0.25

    Mas em equilíbrio, temos

    + W 0.25   ft - k δ ST 1.5   ft = 0

    Por isso

    - k 1.5 2 θ = 7.8125 g + 0.9375 g θ ¨

    - 48   ft/s 1.5 2 θ = 8.75 32.2 θ ¨

    θ ¨ + 397.44 θ = 0

    Passo 3

    Frequência natural e período.

    ω n 2 = 364.11

    ω n = 19.936   rad/s

    τ = 2 π ω n = 2 π 19.936   rad/s

    τ = 2 π ω n = 2 π 19.936   rad/s

    Passo 4

  2. No final B.

x m = 0.4   in.

v m = x m ω n = 0.4   in. 19.936   rad/s = 7.974   in./s

Resposta

a )   τ = 0.315   s

b )   v m = 0.665   ft/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas hastes uniformes AB e CE, cada uma com 1,5 kg de massa e 600 mm de comprimento, são soldadas uma à outra em seus pontos médios. Sabendo que este conjunto tem uma velocidade angular de magnitude c
Um paralelepípedo retangular sólido de massa m tem uma base quadrada de lado a e comprimento 2 a . Sabendo que ele gira a uma taxa constante em torno de sua diagonal AC 'e que sua rotação é observada
(a) Mostre que o momento angular H B de um corpo rígido sobre o Ponto B pode ser obtido adicionando ao momento angular H A desse corpo sobre o Ponto A o produto vetorial do vetor r A / B desenhado de
Um disco fino e homogêneo de massa com raio r gira a uma taxa constante a), sobre um eixo sustentado por uma haste vertical com extremidade em garfo, que gira a uma taxa constante ω 2 . Determine o mo
Um disco homogêneo de peso W = 6 l b gira a uma taxa constante ω 1 = 16 r a d / s em relação ao braço ABC, que é soldado a um eixo DCE girando a uma taxa constante ω 2 = 8 r a d / s . Determine o mome