Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 56
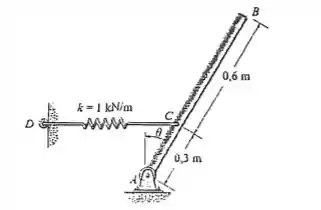
A barra uniforme tem um peso de . Se a mola está livre quando , determine o ângulo para o equilíbrio usando o princípio do trabalho virtual. A mola sempre permanece na posição horizontal devido à guia de rolete em .
Passo 1
Desejamos encontrar o valor de para o equilíbrio a partir do princípio do trabalho virtual. Então, como queremos saber o valor do ângulo vamos converter nossas unidades para evitar trabalhar com números fracionários e facilitar nossas contas. Assim, teremos
Tomemos, agora, as seguintes medidas
Passo 2
Admitindo que
Sendo temos
Além disso, sabemos que quando
Dessa forma, substituindo essas informações na equação anterior, vamos ter
Resposta
Exercícios de Livros Relacionados
O virabrequim está sujeito a um torque M = 50N · m . Determine a força compressiva horizontal F e faça o gráfico de F (ordenada) versus θ , (abscissa) para 0 ≤ θ ≤ 9 0 ° .
Determine o ângulo θ para haver equilíbrio e investigue a estabilidade do mecanismo nessa posição. A mola tem rigidez k = 1,5k N / m e não está deformada quando θ = 90 ° . O bloco A tem massa de 40k g
A junta articulada está sujeita à carga P . Determine a força compressiva F que ela cria sobre o cilindro em A em função de θ .
A mola conectada ao mecanismo não tem deformação quando θ = 90 ° . Determine a posição θ para haver equilíbrio e investigue a estabilidade do mecanismo nessa posição. O disco A é conectado por pino à
A haste uniforme A B tem massa de 50k g . Se as duas molas D E e B C não estão deformadas quando θ = 90 ° , determine o ângulo θ para haver equilíbrio usando o princípio da energia potencial. Investig