Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 97

As barras A B e B C , cada qual de comprimento l e peso desprezível, são unidas a duas molas de constante k cada uma. As molas estão inderformadas e o sistema está em equilíbrio quando θ 1 = θ 2 = 0 . Determine o intervalo de valores de P para os quais a posição de equilíbrio é estavel.

Passo 1

Bom galera, observando a questão nós temos:

x B = l sin ⁡ θ

x C = l sin ⁡ θ 1 + l sin ⁡ θ 2

y C = l cos ⁡ θ 1 + l cos ⁡ θ 2

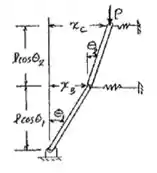
Assim, podemos obter:

V = P y C + 1 2 k x B 2 + 1 2 k x C 2

→ V = P ⋅ l cos ⁡ θ 1 + cos ⁡ θ 2 + 1 2 k l 2 sin 2 ⁡ θ 1 + sin ⁡ θ 1 + sin ⁡ θ 2 2

Passo 2

Belezinha, como você já deve saber, e pra a gente resolver a questão, a gente precisa adotar que para um θ muito pequeno:

θ = sin ⁡ θ

Logo:

θ 1 = sin ⁡ θ 1

θ 2 = sin ⁡ θ 2

1 - 1 2 θ 1 2 = cos ⁡ θ 1

1 - 1 2 θ 2 2 = cos ⁡ θ 2

Então, com isso a gente tem:

V = P ⋅ l 1 - 1 2 θ 1 2 + 1 - 1 2 θ 2 2 + 1 2 k ⋅ l 2 θ 1 2 + θ 1 + θ 2 2

Passo 3

Show de bola, já temos essa equação, e a gente pode pegar derivadas parciais, que ficam assim:

∂ V ∂ θ 1 = - P l θ 1 + k l 2 θ 1 + θ 1 + θ 2 2

∂ V ∂ θ 2 = - P l θ 2 + k l 2 θ 1 + θ 2

Também temos:

∂ 2 V ∂ θ 1 2 = - P l + 2 k l 2

∂ 2 V ∂ θ 2 2 = - P l + k l 2

∂ 2 V ∂ θ 1 ∂ θ 2 = k l 2

Passo 4

Bom, e para as condições de estabilidade temos:

θ 1 = θ 2 = 0

→ ∂ V ∂ θ 1 = ∂ V ∂ θ 2 = 0

→ ∂ 2 V ∂ θ 1 ∂ θ 2 2 - ∂ 2 V ∂ θ 1 2 ∂ 2 V ∂ θ 2 2 < 0

Substituindo o que já temos:

k l 2 2 - - P l + 2 k l 2 - P l + k l < 0

k 2 l 4 - P 2 l 2 + 3 P k l 3 - 2 k 2 l 4 < 0

P 2 - 3 k l P + k 2 l 2 > 0

Resolvendo isso a gente encontra dois resultados:

P < 3 - 5 2 k l = 0,382 k l

E:

P > 3 + 5 2 k l = 2,62 k l

Passo 5

Por fim, temos também que:

∂ 2 V ∂ θ 1 2 > 0

→ - P l + 2 k l 2 > 0

→ P < 1 2 k l

E:

∂ 2 V ∂ θ 2 2 > 0

→ - P l + k l 2 > 0

→ P < k l

Logo, todas as condições de equilíbrio são satisfeitas quando:

0 ≤ P ≤ 0,382 k l

Resposta

0 ≤ P ≤ 0,382 k l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

51- Uma extremidade da mola de torção está presa ao chão em A e a outra extremidade está presa ao eixo em B . A rigidez a torção K da mola elástica é o torque necessário para torcer a mola de um ângul
57- A figura mostra uma cadeira reclinável de escritório juntamente com um detalhe do projeto do mecanismo de inclinação suportado por uma mola. A estrutura do assento é articulada em relação ao ponto
56- Determine por meio de cálculos se o semicilindro homogêneo e a casca semicilíndrica permanecerão nas posições mostradas ou se eles rolarão sobre os cilindros inferiores.
53- O cilindro de massa m e raio r rola sem deslizar sobre a superfície circular de raio ρ . Um pequeno corpo de massa m / 4 está preso ao cilindro. Determine o máximo valor de ρ para o qual o corpo é
54- O hemisfério sólido de diâmetro 2 b e o cilindro concêntrico de diâmetro b estão em repouso sobre uma superfície horizontal. Determine a altura máxima h que o cilindro pode ter sem fazer com que o