Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 111
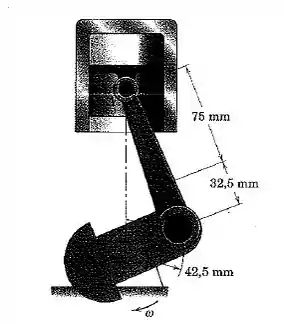
A biela AB de 0,6 kg de um determinado motor de combustão interna possui centro de massa em G e um raio de giração em relação a G de 28 mm. O pistão e o pino A possuem uma massa total de 0,82 kg. O motor está funcionando a uma velocidade constante de 3000 rpm, de modo que a velocidade angular da manivela é de 100π rad/s. Despreze os pesos dos componentes e a força exercida pelos gases de combustão no cilindro em comparação às forças dinâmicas produzidas e calcule o módulo da força sobre o pino do pistão A para o ângulo da manivela θ = 90°. (Sugestão: Utilize a relação alternativa para o momento, com B como o centro para os momentos).
Passo 1
A expressão geral para a aceleração é dada por:
Note que a aceleração pode ser decomposta em duas vertentes, uma tangencial e outra normal, visto a natureza do movimento.
Passo 2
A componente tangencial relativa e a aceleração angular serão determinadas da seguinte forma:
Passo 3
A aceleração em A pode ser descrita por:
Passo 4
No pistão, o diagrama de corpo livre, considerando o sistema de coordenada positivo usual:
Na biela, no ponto B, tem-se pelo somatório dos momentos:
Passo 5
O módulo da força A pode ser obtido em termos de suas componentes:
Resposta
O módulo da força A para as solicitações apresentadas será de 1528,76 N.