Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 212

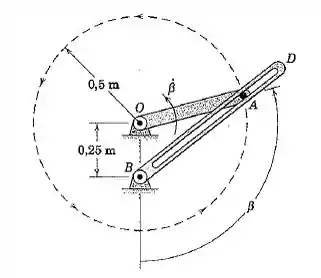
A barra AO gira em torno do ponto fixo O com velocidade constante de 0,8 rad/s. O pino A é fixo na barra AO e está encaixado na ranhura do membro BD, que gira em torno de um eixo através do ponto B. Determine e represente graficamente para todo o intervalo 0 ≤ β ≤ 360° a velocidade angular e a aceleração angular de BD e a velocidade e aceleração do pino A em relação ao membro BD.

Passo 1

A partir do esquema disponível, é interessante a representação do diagrama dinâmico com as informações do sistema de coordenadas e parâmetros geométricos, dessa forma, tem-se:

Com o triângulo formado, pela lei dos Cossenos e lei dos senos, tem-se, respectivamente:

r 2 =   h 2 + R 2 - 2 h r C o s β

s e n ( 90 ° -   θ ) R =   c o s θ R = s e n β r

Note que as decomposições de vetores fornecem uma expressão geral para as grandezas fora da orientação do sistema de coordenadas da seguinte forma:

I   =   c o s θ   i - s e n θ   j

J = s e n θ   i + c o s θ   j

Passo 2

De modo vetorial, tem-se as expressões para a velocidade da seguinte forma

V A =     ω   x   R ⃑

a A =     ω 2   x   R ⃑

De tal forma que o vetor R é decomposto em relação ao sistema de coordenadas adequado à resolução. Portanto:

V A =     ω R * [ - s e n β - 90 ° I + cos ⁡ β - 90 ° J ]

a A =     ω 2 R * [ - c o s β - 90 ° I - sen ⁡ β - 90 ° J ]

Passo 3

Definidos I e J no passo 01, substituindo nas equações resultantes do passo 2, tem-se a seguinte configuração:

V A =     ω R * { - s e n β - 90 ° * c o s θ   i - s e n θ   j + cos ⁡ β - 90 ° * s e n θ   i + c o s θ   j }

a A =     ω 2 R * { - c o s β - 90 ° * c o s θ   i - s e n θ   j - sen ⁡ β - 90 ° * s e n θ   i + c o s θ   j }

Passo 4

Assim, aplicando a ideia de velocidade relativa para BD, tem-se:

V A = V B +   ω   x   r + V r e l

Sabemdo que V B ⃑ = 0 ⃑ e realizando a comparação da equação do passo 4 com a resultante da velocidade do passo 3 em termos das direções das componentes, chega-se às seguintes conclusões:

r ⃑ = r   i ^ V r e l ⃑ = a r e l   i ^ ω ⃑ = ω   k ^

Para a aceleração, sabendo que a B ⃑ = 0 ⃑ :

a A = a B +   α   x   r +   ω   x   ω   x   r + 2 ω   x   V r e l +   a r e l

As conclusões resultantes são:

V r e l =   V A x                               ω =   V A y r                         a r e l =     a A x +   ω ² r                           α   =   ( a A y - 2 ω V r e l ) r

Utilizando um programa, pode-se verificar que graficamente o comportamento é da seguinte maneira:

01. Grandezas angulares

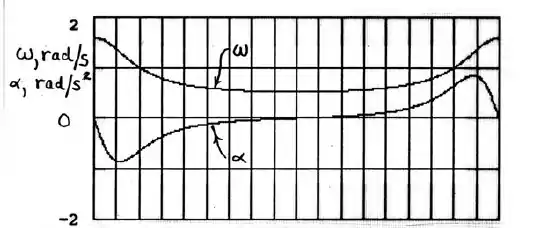
02. Grandezas lineares

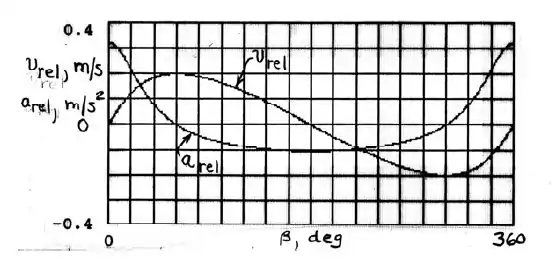
Resposta

Para o intervalo de 0 a 360°, as grandezas solicitadas são calculadas e expressas em forma dos gráficos acima direcionados.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante mostrado, a base do braço robótico gira em torno do eixo z com uma velocidade angular ω 1 = 4 r a d / s , a qual está aumentando a ω ˙ 1 = 3r a d / s 2 . Além disso, a lança B C gira com u
Se a manivela B C gira com uma velocidade angular ω B C = 6r a d / s , determine a velocidade do anel em A . Suponha que a velocidade angular de A B é perpendicular à barra.
A barra A B está fixada aos anéis nas suas extremidades por juntas esféricas. Se o anel A se desloca para cima com uma aceleração a A = 2 km / s 2 , determine a aceleração angular da barra A B e a int
Para o cursor e a manivela do Prob. 5/209 desenvolva a expressão para a aceleração a A do pistão (admitida positiva para a direita) como uma função de θ para ω = θ ˙ = c o n s t a n t e . Substitua os
Um torque constante M ultrapassa o momento em torno de O devido à força F sobre o embolo, e resulta em uma aceleração angular θ ¨ = 100 1 - c o s θ r a d / s 2 . Se a manivela AO é liberada a partir d