Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 207
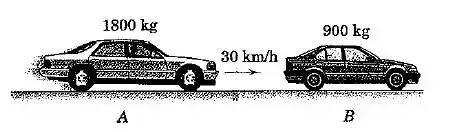
O carro está inicialmente parado e é atingido pelo carro que se desloca com velocidade inicial . Os carros ficam presos e se deslocam juntos com velocidade após a colisão. Se o tempo de duração da colisão é , determine (a) a velocidade final comum , (b) a aceleração média de cada carro durante a colisão, e (c) o módulo da força média exercida por um carro sobre o outro durante o impacto. Todos os freiso estão soltos durante a colisão.
Passo 1
(a) Para calcular a velocidade final do conjunto, podemos aplicar a conservação de momento linear:
E nessa conta nós consideramos que os dois carros continuam juntos após a colisão.
Passo 2
A aceleração média de cada carro durante a colisão pode ser calculada usando essa fórmula:
A colisão durou cerca de , e as variações de velocidade foram:
E então as acelerações médias são:
Passo 3
Agora o módulo da força média pode ser calculando simplesmente usando a segunda lei de Newton:
Além disso, pela terceira lei de Newton, sabemos que a força sobre os dois carros tem o mesmo módulo, então podemos usar qualquer um dos dois para calcular :
Resposta
(a)
(b) e
(c)