Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 171

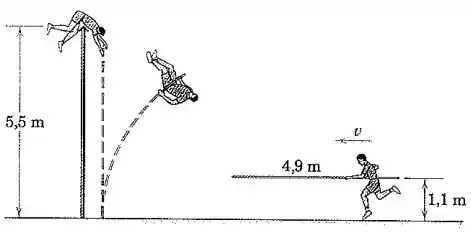
Um atleta de salto com vara de 80   k g carregando uma vara uniforme de 4,9   m e 4,5   k g se aproxima do salto com uma velocidade v e ultrapassa por pouco o sarrafo colocado a uma altura de 5,5   m . Quando ele ultrapassa o sarrafo, sua velocidade e a da vara são essencialmente nulas. Calcule o valor mínimo possível de v necessário para ele realizar o salto. Tanto a vara horizontal quanto o centro de gravidade do saltador estão a 1,1   m acima do nível do solo durante a aproximação.

Passo 1

Aqui teremos conservação da energia mecânica, então:

T 1 + V 1 = T 2 + V 2

Inicialmente, o atleta A e a vara V têm a mesma velocidade v , então:

T 1 = 1 2 m A + m V v 2 = 1 2 80 + 4,5 v 2 = 42,25 v 2

Além disso, o centro de massa de ambos estão a 1,1   m do chão:

V 1 = m A + m V g 1,1 = 80 + 4,5 9,81 1,1 = 911,8   J

Passo 2

Na posição final, ambos têm velocidade nula, ou seja,

T 2 = 0

Porém, o centro de massa do atleta chega a 5,5   m do chão, enquanto o centro de massa da vara fica a uma altura menor que essa. Assumindo que a massa se distribui uniformemente pelo comprimento da vara, e que ela fica completamente vertical, tocando o chão, seu centro de massa fica a 4,9 / 2     m do chão:

V 2 = m A g 5,5 + m V g 4,9 2 = 80 9,81 5,5 + 4,5 9,81 4,9 2 = 4424,6   J

Passo 3

Agora que temos todos os valores de energia de antes e depois, determinaremos a velocidade v :

T 1 + V 1 = T 2 + V 2

42,25 v 2 + 911,8 = 0 + 4424,6

v = 9,118   m / s

v = 32,8   k m / h

Resposta

v = 32,8   k m / h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força F = x i + y j + z k x 2 + y 2 + z 2 3 / 2 age sobre uma partícula P x , y , z que se move no espaço. (a) Usando a relação deduzida no Problema 13.79, mostre que essa força é uma força conserva
(a) Calcule o trabalho feito de D a O para a força P do Problema 13.82 por integração ao longo da diagonal do cubo. (b) Usando o resultado obtido na resposta da parte b do Problema 13.82, verifique qu
Uma força F age sobre uma partícula P x , y que se move no plano x y . Determine se a força F é uma força conservativa e calcule o trabalho de F quando P descreve a trajetória no sentido horário A , B
Um satélite é posto em uma órbita elíptica em torno da Terra. Sabendo-se que a razão v A / v P entre as velocidades no apogeu A e no perigeu P é igual à razão r P / r A , entre as distâncias de P e A
Enquanto descreve uma órbita circular a 300 km acima da Terra, um veículo espacial lança um satélite de comunicação de 3.600 kg. Determine (a) a energia adicional necessária para pôr o satélite em uma