Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 25
Uma força constante P é aplicada a um pistão e haste de massa total m para fazê-los se mover em um cilindro cheio de óleo. Conforme o pistão se move, o óleo é forçado através dos orifícios no pistão e exerce no pistão uma força de magnitude em uma direção oposta ao movimento do pistão. Sabendo que o pistão começa do repouso em t = 0 e x = 0, mostre que a equação que relaciona x, v e t, onde x é a distância percorrida pelo pistão e v é a velocidade do pistão, é linear em cada das variáveis.
Passo 1
Vamos esboçar as forças atuantes no pistão para realizar o somatório das forças:D
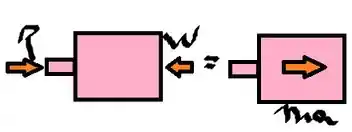
Passo 2
Para a obtenção da posição temos :D
, que é linear
Resposta
Exercícios de Livros Relacionados
A esfera homogênea do Prob. 6/196 é colocada sobre a inclinação com uma velocidade angular no sentido horárioω o , mas sem velocidade linear em seu centro ( v o = 0 ) . Determine o tempo de duração t
O módulo de pouso lunar de 17,5t com centro de massa G tem um raio de giração de 1,8m em relação a G . O módulo é projetado para pousar na superfície lunar com uma velocidade vertical de queda livre d
Uma professora de dinâmica com 55k g está demonstrando os princípios da quantidade de movimento angular para sua classe. Ela fica de pé sobre uma plataforma que gira livremente com seu corpo alinhado
Cada uma das duas barras uniformes A de 300m m possui uma massa de 1,5k g e é articulada em sua extremidade à base B que está girando. A base com 4k g tem um raio de giração de 40m m e está inicialmen
A roda de 30k g tem um raio de giração em relação a seu centro de 75m m e está girando no sentido horário na taxa de 300r p m , quando é liberada no plano inclinado sem velocidade em seu centro O . En