Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 138
Um modelo simplificado baseado em uma linha reta deve ser obtido para a variação de pressão dentro do cano de um rifle de 10 mm de diâmetro durante o disparo de uma bala de 20 g. Sabendo que leva 1,6 ms para a bala percorrer o comprimento do cano e que a velocidade da bala na saída é de 700 m/s, determine o valor de
Passo 1
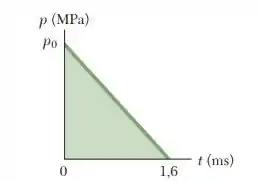
E vamos resolver mais uma questão envolvendo gráficos. Sem problemas. Mesmo trabalhando com a pressão, devemos lembrar que ela está relacionada com a força pela relação
Onde A é a área onde a força é aplicada. Observando o gráfico, que é uma reta, podemos chegar a uma função entre a pressão e o tempo. Uma função de primeiro grau é representada por:
Para t = 0,
Para t = 1,6 ms
Assim a função p(t) será:
Passo 2
Força em função do tempo remete ao princípio do impulso. Para uma força em função do tempo, temos que:
Para o nosso caso:
Passo 3
Agora vamos substituir os valores para área, velocidade e massa. A área de seção do cano é:
Assim