Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 84

Determine a vazão Q no canal do Problema 14.83 sabendo que b = 3,6 m, d 1 = 1,2 m e d 2 = 1,5 m.

Passo 1

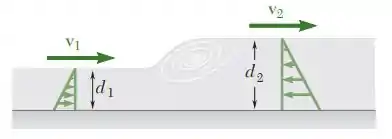
Vamos lá resolver mais essa? Aqui temos um escoamento de água em um canal, onde sua profundidade aumentou devido a um ressalto hidráulico. Pelo princípio da conservação da massa temos que:

Q 1 = Q 2 = Q

Colocando isso em termos de vazão mássica:

Δ m Δ t = ρ Q → Q = 1 ρ ρ b d v = b d v

Assim,

v 1 = Q b d 1                   v 2 = Q b d 2

Como a velocidade em 1 é diferente da velocidade em 2, essa variação foi causada pela variação de pressão entre essas duas seções. Assim usaremos o princípio de impulso e quantidade de movimento para obtermos a vazão Q. Antes, vamos descobrir a pressão em cada seção:

p 1 = ρ g h = ρ g d 1

p 2 = ρ g d 2

A força de impulso de cada seção é calculada como:

F 1 = 1 2 ρ g d 1 b d 1 = 1 2 ρ g b d 1 2

F 2 = 1 2 ρ g b d 2 2

Passo 2

Agora, utilizando o esquema abaixo que descreve o princípio do impulso e da quantidade de movimento:

Δ m v 1 + F 1 Δ t - F 2 Δ t = Δ m v 2

Δ m Δ t v 1 - v 2 =   F 2 - F 1

ρ Q Q b d 1 - Q b d 2 = 1 2 ρ g b d 2 2 - d 1 2

Q 2 d 2 - d 1 b d 1 d 2 = 1 2 g b ( d 2 + d 1 ) ( d 2 - d 1 )

Q = b 1 2 g d 1 d 2 d 1 + d 2

Passo 3

Substituindo os valores fornecidos no enunciado da questão temos:

Q = b 1 2 g d 1 d 2 d 1 + d 2

Q = 3,6 1 2 9,81 1,2 1,5 1,2 + 1,5

Q = 17,58   m 3 / s

Resposta

Q = 17,58 m³/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14.43. Um bloco B de 20 kg é suspenso por uma corda de 2 m fixada em um carrinho A de 30 kg, que pode rolar livremente sem atrito no caminho horizontal. Se o sistema é liberado do repouso na posição m
14.30. Mostre que a relação ∑ m A = H ˙ A ' , onde H’A é definido pela Eq. (1) do Problema 14.29 e ∑ M A representa a soma dos momentos em relação a A das forças externas que atuam sobre o sistema de
14.39 Em um jogo de bilhar, a bola A se desloca com uma velocidade v0 de intensidade v0 5 m/s quando ela atinge as bolas B e C, que se encontram em repouso e alinhadas como mostrado na figura. Sabendo
14.44. Três esferas, cada uma de massa m, podem deslizar livremente sobre uma superfície horizontal sem atrito. As esferas A e B estão ligadas por um fio inextensível e inelástico de comprimento l e e
14.45. Um veículo espacial de 360 kg deslocando-se com velocidade v0 (450 m/s)k passa pela origem O. Cargas explosivas dividem, então, o veículo em três partes, A, B e C, com massas de 60 kg, 120 kg e