Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 37
Um bloco de bronze (não magnético) de 300 g e um ímã de aço de 200 g estão em equilíbrio em um tubo de bronze forçado sob a força magnética repulsiva de um outro ímã de aço localizado a uma distância de . A força é inversamente proporcional ao quadrado da distância entre e . Se o bloco for subitamente removido, determine (a) a velocidade máxima de e (b) a aceleração máxima de . Considere que a resistência do ar e o atrito sejam desprezíveis.
Passo 1
Vamos lá! Como estamos em um capítulo que trabalha com trabalho e energia, vamos utilizar esta metodologia para resolver esta questão!
A parte mais difícil desta questão é a identificação da força magnética . Mas não precisam se assustar, pois aqui não precisaremos calcular estas forças através das leis da Física. O que devemos fazer é relacionar a força conhecida (para ) com uma força a uma distância qualquer.
Mas, para isto, nosso primeiro passo é construir um diagrama de corpo livre. Então, fazendo o diagrama de corpo livre, temos,
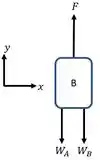
Passo 2
No enunciado da questão, foi nos dito que, quando a distância for , o bloco está em equilíbrio. Este é o nosso gancho para descobrirmos a relação da força magnética .
Então, como o bloco está em equilíbrio, o somatório das forças é igual a zero. Logo,
Só que esta força é para . Como a força é inversamente proporcional ao quadrado da distância , então, a relação da força em função de é:
E agora sim podemos partir em si para a nossa questão de dinâmica!
Passo 3
Agora vamos supor que o bloco é retirado subitamente. Assim, o bloco que estava em repouso começará a se movimentar.
Na letra a) precisamos determinar a velocidade máxima atingida pelo bloco. Esta velocidade será no ponto em que a taxa de variação do trabalho no bloco for igual a zero.
Até aí tudo bem. Mas quem é a relação do trabalho? Calculando-o, temos:
E assim, temos que o ponto em que a variação de trabalho é igual a zero é:
Passo 4
Agora que sabemos o ponto de velocidade máxima, basta utilizarmos o princípio de trabalho e energia para calcularmos ela. Para isto, vamos precisar dos termos de energia cinética. Eles serão:
Aplicando o princípio do trabalho e energia, quando , temos:
E assim finalizamos a letra a).
Passo 5
Agora vamos para a letra b). Aqui precisamos determinar a aceleração máxima no bloco . Aqui é mais simples. Isto irá ocorrer quando a força resultante for máxima, o que ocorrerá logo no início, devido a maior intensidade da força magnética.
Portanto, fazendo o somatório de forças para o ponto , vamos obter o seguinte valor da aceleração:
E assim finalizamos a nossa questão.