Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 119
A placa retangular uniforme tem uma massa de e é sustentada no plano vertical pelas duas hastes paralelas de massa desprezível e pelo cabo . Se o cabo se rompe de repente, determine a velocidade angular das hastes pouco antes que a placa atinja a superfície horizontal . Encontre também a força no elemento no mesmo instante.
Passo 1
Conforme a placa cai, a energia potencial gravitacional que ela tinha no início vai se converter em energia cinética.
Então, como a placa parte do repouso, e termina em uma altura que podemos definir como o zero da nossa energia potencial, vamos escrever a seguinte equação:
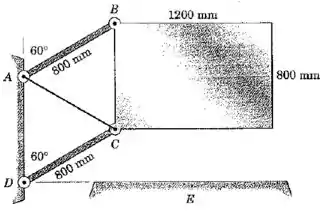
E a altura percorrida pelo centro de massa (ou qualquer outro ponto) da placa até atingir a superfície pode ser calculada diretamente a partir do desenho:
Então:
E a velocidade angular associada a é:
Passo 2
Agora vamos calcular a força no elemento no instante imediatamente anterior à colisão.
Uma boa forma de fazer isso é escrever uma equação de momentos em relação ao ponto . Considerando que o centro de massa faz uma trajetória curvilínea, e não tem aceleração angular em torno de :
Dessa forma vamos anular o momento da força nesse braço, e ficaremos apenas com o momento da força peso e da força que queremos calcular.
Passo 3
E para escrever o termo da direita, precisamos escrever as componentes tangencial e centrípeta da aceleração do centro de massa.
A componente tantencial está a uma distância perpendicular do ponto , e a componente centrípeta está a
E a aceleração tangencial é simplesmente a aceleração da gravidade:
Então:
Resposta
A velocidade angular será , e a força no elemento é de .