Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.7 - Ex. 79
Um rolo de cabo flexível pesado com um comprimento total de metros e uma massa de deve ser estendido ao longo de uma linha reta horizontal. A extremidade está presa a uma estaca em , e o cabo se solta do rolo e sai através da abertura horizontal no carrinho como mostrado. O carrinho e o tambor juntos possuem uma massa de . Se o carrinho está se deslocando para a direita com uma velocidade de quando metros de cabo permanecem no tambor e a tração da corda na estaca é , determine a força necessária para dar ao carrinho e ao tambor uma aceleração de . Despreze totalmente o atrito.
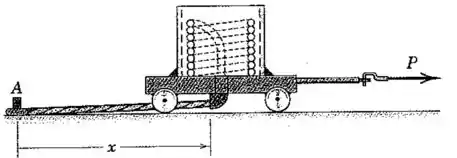
Passo 1
Vamos começar olhando para a equação que dá a soma das forças externas sobre o carrinho:
Nesse caso as duas forças são as seguintes: a tração da corda puxando para a esquerda na horizontal, e a força puxando para a direita:
E queremos considerar isso no instante em que a tração da corda é:
Passo 2
E como a ideia é produzir uma aceleração de para a direita, já podemos dizer que:
E queremos considera isso no instante em que a velocidade do carrinho é:
E metros do cabo ainda estão dentro do tambor. Como cada metro de cabo tem uma massa de , a massa do carrinho nesse instante é:
E agora só falta encontrar uma expressão para a taxa de variação da massa. Bom, o carrinho se move por metros a cada segundo, e cada metro da corda tem , então:
Passo 3
Agora podemos substituir tudo na equação do passo :
Resposta
A força necessária é .