Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 70

Sabendo que as barras possuem o mesmo comprimento l e o peso da engrenagem em AB é de 13,5N e o da engrenagem da barra CD é 9N, determine as posições de equilíbrio do sistema e determine em cada caso a estabilidade do equilíbrio:

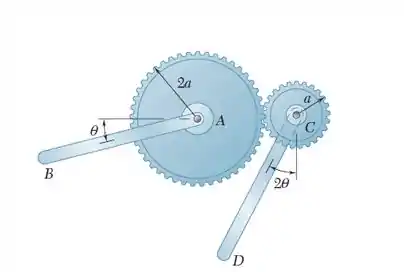
Passo 1

Fala aí galera, vamos para mais um problema de estática. Sabemos que para encontrar a posição de equilíbrio, devemos encontrar a expressão da energia potencial e igualar sua derivada a 0. Logo, sabemos que:

V A B = m   g   h = 13,5   × l cos ⁡ 2 θ = 13,5 l c o s ( 2 θ )

V C D = m   g   h = 9   × l cos ⁡ 2 θ = 9 l c o s ( 2 θ )

Logo, a energia potencial total será:

V = 9 + 13,5 l c o s 2 θ = 22,5 l c o s 2 θ

Vamos agora derivar a expressão:

V ' = 22,5 l × - 2 s e n 2 θ = - 45 l s e n 2 θ

Igualando a 0, teremos:

- 45 l s e n 2 θ = 0

θ = π   ;   θ = 0

Portanto, as posições de equilíbrio são para estes 2 valores de θ .

Passo 2

Já para determinar a estabilidade das barras, precisamos estudar o sinal da segunda derivada. Logo:

V ' ' = - 90 l c o s 2 θ

Já temos as situações de equilíbrio calculadas no passo 1, logo, vamos substituir para que possamos determinar a estabilidade da seguinte maneira:

E s t á v e l → V ' ' > 0

I n s t á v e l → V ' ' < 0

N e u t r o → V ' ' = 0

Portanto:

θ = π → V ' ' = 90 l → E s t á v e l

θ = 0 → V ' ' = - 90 l → I n s t á v e l

Resposta

θ = π → E s t á v e l

  θ = 0 → I n s t á v e l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se  a  função de potencial de um  sistema conservativo com um grau de liberdade é  V = ( 12 sin ⁡ 2 θ + 15 cos ⁡ θ ) J , onde  0 °θ180 ° , determine as posições de equilíbrio e investigue a estabilida
Se  a  função de potencial de um  sistema conservativo com um grau de liberdade é  V = ( 8 x 3 - 2 x 2 - 10 ) J , onde  x é dado em metros, determine as posições de equilíbrio e investigue a estabilid
A  mola  da  balança  tem  um  comprimento  a quando  não  deformada.  Determine  o  ângulo  θ   de  equilíbrio quando o peso  W  é suportado na plataforma. Despreze  o  peso  dos  elementos. Que  val
A  haste uniforme tem 80k g de massa.  Determine  o  ângulo  θ   de  equilíbrio e investigue a sua estabilade quando estiver nessa posição A mola não está deformada quando  θ = 90 ° ?
Se  a  função de potencial de um  sistema conservativo com um grau de liberdade é  V = ( 10 cos ⁡ 2 θ + 25 sin ⁡ θ ) J , onde  0 °θ180 ° , determine as posições de equilíbrio e investigue a estabilida