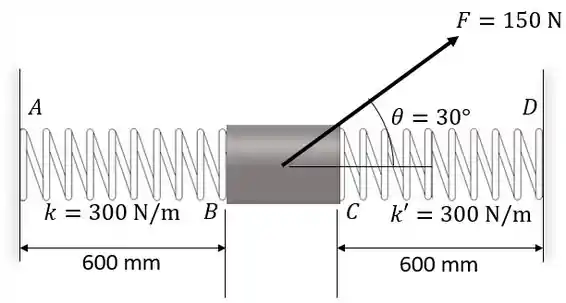
As molas e têm rigidez e , respectivamente, e as duas molas têm comprimento não deformado de 600 mm. Se o anel liso de 2 kg parte do repouso quando as molas não estão deformadas, determine a velocidade do anel quando ele tiver se deslocado 200 mm.

O enunciado nos dá as seguintes informações:

Rigidez da mola : ;

Rigidez da mola : ;

Comprimento não deformado das molas: ;

Deslocamento: ;

Massa do anel: .

Como o anel parte do respouso, sua velocidade inicial . Além disso, nesse instante as molas não estáo deformadas.

A partir dai, devemos determinar a velocidade do anel quando ele tiver se deslocado 200 mm.

Pela imagem, vemos que uma força é aplicada ao anel.

Vamos desenhar o diagrama de corpo livre do anel para entender melhor o que está acontecendo:

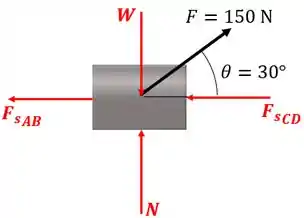
Onde é a foça peso, é a força normal, e são as forças exercidas pelas molas e , respectivamente.

Devido a ação da força , a mola será comprimida e a mola será expandida. Por esse motivo a direção das forças das molas foi desenhada desta forma.

Como o anel se deslocará somente na horizontal, somente as forças nesta direção realizarão trabalho sobre ele. Estas são: , e .

Somente atua no mesmo sentido do deslocamento do anel, logo o trabalho realizado por esta força será positivo. O trabalho realizado pelas forças das molas serão negativos pois atuam no sentido oposto ao movimento do anel.