Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 140
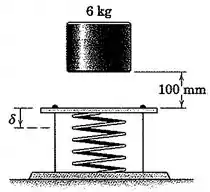
3/140) O cilindro de é liberado a partir do repouso na posição mostrada e cai sobre a mola , que foi inicialmente pré-comprimida em pela trava leve e fios restritivos . Se a rigidez da mola é de , calcule a deflexão adicional da mola produzida pela queda do cilindro antes que este reverta o movimento .
Passo 1
Então pessoal , aplicando a lei de trabalho-energia , temos que :
Logo ,
Substituindo os valores que conhecemos :
Passo 2
Bom galera, aplicando a distributiva e resolvendo a integral definida , achamos que :
Resolvendo a equação do segundo grau acima , obtemos como único valor viável :
O outro resultado é negativo , sendo assim , não faz sentido e não é considerado .
Resposta
E aí , Topam resolver mais questões com a gente ?
Exercícios de Livros Relacionados
A viga fina, tendo uma massa de 75 kg, é suportada por dois cabos. Se o cabo na extremidade B é cortado, de modo que a viga seja liberada do repouso quando θ = 30 ° , determine a velocidade com que a
A bobina tem uma massa de 100 kg e raio de giração de 400 mm em relação a seu centro de massa O. Se ela é liberada do repouso, determine sua velocidade angular após seu centro O haver descido pelo pla
A bobina tem uma massa de 100 kg e raio de giração de 400 mm em relação a seu centro de massa O. Se ela é liberada do repouso, determine sua velocidade angular após seu centro O haver descido pelo pla
O cilindro A, de 25 kg, está descendo a uma velocidade de 6 m/s quando o freio é acionado. Se a roda B deve ser parada após haver girado cinco revoluções, determine a força constante P, que deve ser a
A bobina tem uma massa de 60k g e raio de giração k G = 0,3m . Se ela é liberada do repouso, determine a que distância seu centro desce pelo plano liso, antes de atingir uma velocidade angular de ω =