O carro esportivo tem uma massa de 1,5 Mg e um centro de massa em G. Determine o tempo mais curto que ele leva para alcançar uma velocidade de 80 km/h, partindo do repouso, se o motor impulsiona somente as rodas traseiras, enquanto as rodas dianteiras estão rodando livremente. O coeficiente de atrito estático entre as rodas e a estrada é . Despreze a massa das rodas para o cálculo. Se a potência motriz pudesse ser fornecida a todas as quatro rodas, qual seria o tempo mais curto para o carro alcançar uma velocidade de 80 km/h?
Passo 1
Para resolver esse exercício, iremos primeiramente determinar quais são as equações do movimento que governam o sistema, e depois aplica-las aos dois casos, fazendo as devidas observações.
Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².
Como ponto de partida, escrevemos todas as equações de movimento do sistema com o auxílio do esquema a seguir:
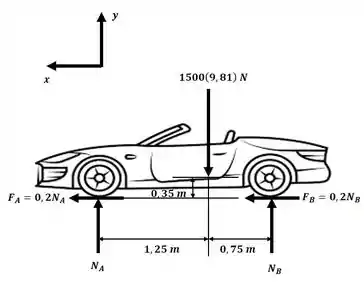
Passo 2
Iremos analisar primeiro o caso onde o motor impulsiona somente as rodas traseiras, ou seja, , logo, da segunda equação do passo 1, temos:
Observe que , a reação existe, só não temos atrito estático nesse ponto. Agora, da terceira equação do passo 1:
Agora, substituindo esse valor na primeira equação, encontraremos o valor da aceleração do centro de massa:
Por fim, podemos usar a equação da velocidade para encontrar o tempo necessário para acelerar o carro até a velocidade final:
Devemos lembrar de converter a velocidade, que está em km/h para m/s:
Passo 3
Agora, analisaremos o caso onde a potência é fornecida a todas as quatro rodas, da segunda equação do passo 1, temos:
Substituindo esse valor na terceira equação do passo 1:
Sendo assim, o valor de é dado por:
E, substituindo esses valores na primeira equação, encontraremos a aceleração:
E, por fim, substituindo o valor da aceleração na equação da velocidade: