Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 118
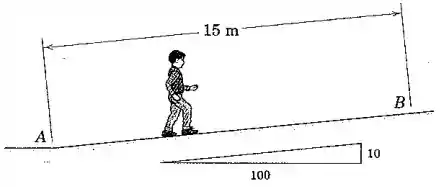
Um menino de parte do repouso na base de uma inclinação de e aumenta sua velocidade em uma taxa constante até quando passa em , ao longo da inclinação a partir de . Determine sua potência de saída quando ele atinge .
Passo 1
Primeiramente, vamos calcular qual é a aceleração (constante) do menino, usando a seguinte equação do movimento uniformemente acelerado:
Agora, note que uma inclinação de equivale ao ângulo:
Passo 2
Então, usando a Segunda Lei de Newton, calculamos a força que o menino faz na direção da subida:
Em , a potência de saída do menino pode ser dada por:
Resposta
Exercícios de Livros Relacionados
O veículo é utilizado para transportar suprimentos subindo e descendo a inclinação de 25 % . Cada par de rodas, um em A e outro em B , tem uma massa de 140k g com um raio de giração de 150m m . O tamb
Um sistema de engrenagens planetárias é apresentado, onde os dentes das engrenagens são omitidos da figura. Cada uma das três engrenagens planetárias idênticas A , B e C tem uma massa de 0,8k g , um r
A torre aérea mostrada é projetada para elevar um operário em uma direção vertical. Um mecanismo interno em B mantém o ângulo entre A B e B C igual a duas vezes o ângulo θ entre B C e o solo. Se a mas
Um pequeno carro híbrido de 1.300 kg está viajando a 108 km/h. Determine (a) a energia cinética do veículo, (b) a velocidade escalar para um caminhão de 9.000 kg que tem a mesma energia cinética que o
Partindo do repouso, uma pedra de 4 kg cai de uma altura h e bate no chão com uma velocidade de 25 m / s . (a) Encontre a energia cinética da pedra quando ela bate no chão e a altura h da queda. (b) R