Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 145
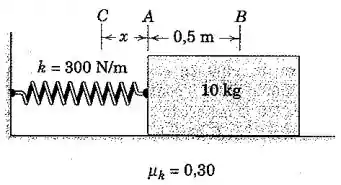
O bloco de é liberado a partir do repouso sobre a superfície no ponto , onde a mola foi esticada por uma distância de a partir de sua posição neutra . O coeficiente de atrito dinâmico entre o bloco e o plano é de . Calcule
(a) a velocidade do bloco quando este passa o ponto e
(b) a distância máxima para a esquerda de que o bloco alcança.
Passo 1
(a) Pessoal, as forças que irão realizar trabalho nesse caso são as forças de atrito e da mola:
Igualamos o trabalho total à variação da energia cinética:
Passo 2
(b) Quando o bloco atingir esse ponto, sua variação de energia cinética é nula, pois lembre-se de que ele começou no repouso. Sendo assim,
Desprezando a solução negativa da equação acima, obtemos:
Resposta
(a)
(b)
Exercícios de Livros Relacionados
O tacômetro mecânico mede a velocidade de rotação N do eixo pelo movimento horizontal do cursor B ao longo do eixo que gira. Esse movimento é causado pela ação centrífuga das duas massas A de 350 g, q
A plataforma móvel de trabalho é elevada por meio de dois cilindros hidráulicos articulados nos pontos C. A pressão em cada cilindro produz uma força F. A plataforma, o homem e a carga têm uma massa c
Cada um dos três painéis idênticos uniformes de uma porta industrial segmentada tem massa m e é conduzido nos trilhos (um mostrado em linha tracejada). Determine a aceleração horizontal a do no painel
O setor e as rodas vinculadas são liberados a partir do repouso na posição mostrada no plano vertical. Cada roda é um disco circular maciço com uma massa 5 k g e rola sobre a trajetória circular fixa
O braço uniforme O A tem uma massa de 4k g , e a engrenagem D tem uma massa de 5k g com um raio de giração ao centro de 64m m . A engrenagem maior B é fixa e não pode girar. Se o braço e a engrenagem