Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 26

Um bloco de 5 kg é fixado a uma mola indeformada de constante k = 2.100 N/mm. Os coeficientes de atrito estático e cinético entre o bloco e o plano são 0,60 e 0,40 respectivamente. Se a força F   é lentamente aplicada no bloco até a tração na mola alcançar 100   N e então subitamente retirada, determine (a) a velocidade do bloco quando este volta a sua posição inicial, (b) a máxima velocidade alcançada pelo bloco.

Passo 1

E aí, ferinha!?! Tudo blz? Neste exercício devemos calcular a velocidade com que um bloco ligado a uma mola retorna a sua posição original após ser esticado (item a) e a máxima velocidade alcançada por esse bloco (item b).

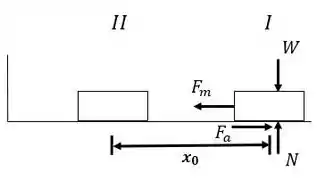
(a) Observando a figura acima, devemos encontrar, inicialmente, o valor de x 0 .

F m = k x 0

x 0 = 100 2100 = 0,0476   m m

Agora podemos calcular a velocidade.

T 2 = 1 2 ⋅ m ⋅ v 2 2 = 1 2 ⋅ 5 ⋅ v 2 2 = 2,5 v 2 2

U 1 → 2 = ∫ x 0 0 - F m d x + F a k ( - x 0 )

F a k = F a = μ ⋅ N = 0,4 5 ⋅ 9,81 = 19,62

U 1 → 2 = - 2100 x 2 2 0 x 0 + ( 19,62 ) ( - 0,0476 )  

U 1 → 2 = 1050 0,0476 2 + ( 19,62 ) ( - 0,0476 )

U 1 → 2 = 1,445

T 1 + U 1 → 2 = T 2

0 + 1,445 = 2,5 v 2 2

v 2 2 = 1,445 2,5

v 2 = 0,76   m / s

(b) Para calcularmos a máxima velocidade alcançada por esse bloco, devemos fazer da seguinte maneira:

Semelhante ao item (a), temos

T 2 = 1 2 ⋅ m ⋅ v 2 2 = 1 2 ⋅ 5 ⋅ v 2 2 = 2,5 v 2 2

Agora a posição varia de x 0 a x .

U 1 → 2 = ∫ x 0 x - F m d x + ∫ x 0 x F a d x

U 1 → 2 = 2100 x 2 2 x x 0 + F a ( x - x 0 )

U 1 → 2 = 1050 [ 0,0476 2 - x 2 ] + ( 19,62 ) ( x - 0,0476 )

T 1 + U 1 → 2 = T 2

0 + 1050 [ 0,0476 2 - x 2 ] + ( 19,62 ) ( x - 0,0476 ) = 2,5 v 2 2

Para v m á x :

d v 2 d x = 0

- 2100 ⋅ x + 19,62 = 0

x = 0,0093   m

1050 [ 0,0476 2 - 0,0093   2 ] + ( 19,62 ) ( 0,0093   - 0,0476 ) = 2,5 v m á x 2

2,5 v m á x 2 = 1,5365

v m á x = 0,78   m / s

Resposta

(a) 0,76   m / s

(b) 0,78   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O mecanismo é constituído por duas barras esbeltas e se move no plano horizontal sob influência da força P . A barra O C tem uma massa m e a barra A C tem massa 2 m . O bloco deslizante em B tem massa
163. Cada uma das barras uniformes O A e O B possui uma massa de 2k g e é articulada livremente em O ao eixo vertical, que recebe uma aceleração constante a = g / 2 . As hastes que conectam o cursor l
O tacômetro mecânico mede a velocidade de rotação N do eixo pelo movimento horizontal do cursor B ao longo do eixo que gira. Esse movimento é causado pela ação centrífuga das duas massas A de 350 g, q
A plataforma móvel de trabalho é elevada por meio de dois cilindros hidráulicos articulados nos pontos C. A pressão em cada cilindro produz uma força F. A plataforma, o homem e a carga têm uma massa c
Cada um dos três painéis idênticos uniformes de uma porta industrial segmentada tem massa m e é conduzido nos trilhos (um mostrado em linha tracejada). Determine a aceleração horizontal a do no painel