Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.7 - Ex. 167

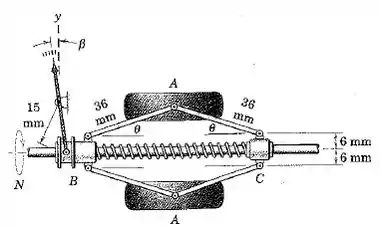
O tacômetro mecânico mede a velocidade de rotação N do eixo pelo movimento horizontal do cursor B ao longo do eixo que gira. Esse movimento é causado pela ação centrífuga das duas massas A de 350 g, que giram com o eixo. O cursor C está preso ao eixo. Determine a velocidade de rotação N do eixo para uma leitura β = 15°. A rigidez da mola é de 900 N/m e está sem compressão quando θ = 0e β = 0. Despreze os pesos das hastes.

Passo 1

O raio para cada peso pode ser escrito como:

r   =   0,006   +   0,036 *   s e n θ

Passo 2

A parcela referente à energia cinética é determinada por:

δ T = 2   m * r * ω 2 -   δ r

Sabendo que:

δ r = 0,036 * cos ⁡ θ

2 * 0,036   -   2 * 0,036 * cos ⁡ θ = 0,015 * s e n   15 °

cos ⁡ θ = 0,946

θ = 18,9 °

Aplicando as substituições, temos que:

δ T = 2   0,35 * ( 0,006   +   0,036 *   s e n θ ) * ω 2 ( -   0,036 * cos ⁡ θ )   δ θ

δ T = 2   0,35 * ( 0,006   +   0,036 *   s e n 18,9 ° ) * ω 2 * ( -   0,036 * cos ⁡ 18,9 ° )   δ θ

δ T = - 0,000421 ω 2   δ θ

Passo 3

Para a energia potencial:

δ V e = k * δ x

δ V e = 900 * ( 2 * 0,036 * 1 - c o s θ * δ [ 2 * 0,036 * 1 - c o s θ ]

δ V e = 4,6656 * 1 - c o s θ * s e n θ   δ θ

δ V e = 4,6656 * 1 - c o s 18,9 ° * s e n 18,9 °   δ θ

δ V e = 0,08148   δ θ

Passo 4

Aplicando na equação geral do balanço energético, tem-se:

δ U =   δ V e +   δ T

Como os pesos são desprezados, δ U = 0 . Portanto:

δ V e +   δ T = 0

0,08148   δ θ   - 0,000421 ω 2   δ θ = 0  

ω = 13,91 r a d / s

ω = 13,91 * 60 2 π

ω = 132,85   R P M ≅ 133   R P M

Resposta

A rotação do eixo para a leitura quando β = 15° será de aproximadamente 133 RPM.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco de 50 kg é transportado por uma distância curta, usando-se dois rolos cilíndricos, cada um com massa de 17,5 kg. Se uma força horizontal P = 125 N é aplicada ao bloco, determine a velocidade d
Quando uma força P = 150 N é aplicada à alavanca do freio, o cilindro A, de 25 kg, está descendo a uma velocidade de 6 m/s. Determine o número de revoluções que a roda B rotacionará antes que seja par
A montagem consiste de duas barras finas de 7,5 kg e de um disco de 10 kg. Se a mola não está deformada quando θ = 45 ° e a montagem é liberada do repouso nessa posição, determine a velocidade angular
A porta uniforme tem massa de 20 kg e pode ser tratada como uma placa fina, tendo as dimensões mostradas na figura. Se ela está conectada a uma mola torsional em A, que tem rigidez k = 80N . m / r a d
A viga fina, tendo uma massa de 75 kg, é suportada por dois cabos. Se o cabo na extremidade B é cortado, de modo que a viga seja liberada do repouso quando θ = 30 ° , determine a velocidade com que a