163. Cada uma das barras uniformes e possui uma massa de e é articulada livremente em ao eixo vertical, que recebe uma aceleração constante . As hastes que conectam o cursor leve às barras possuem massas desprezíveis, e o cursor desliza livremente sobre seu eixo. A mola possui uma rigidez e está sem compressão para o posição equivalente a . Calcule o ângulo assumido pelas barras na condição de aceleração constante.

Passo 1
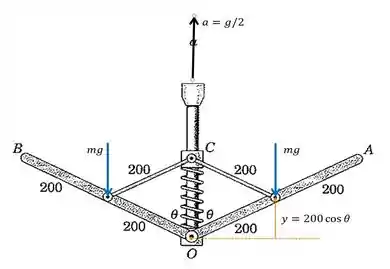
Primeiramente vamos fazer a representação do nosso sistema, posicionando-o com as forças e aceleração atuantes, de modo que possa auxiliar nossa interpretação:
Passo 2
Em seguida, como trata-se de um movimento infinitesimal, vamos tratar de usar a equação de trabalho e energia correspondetes:
Da figura que esboçamos no , podemos ver claramente que o único tipo de energia proveniente na condição inicial, é a potencial , a qual é proveniente das duas forças peso que ilustramos:
Substituindo os valores numéricos que já temos, chegamos ao seguinte valor:
Só que da figura tiramos que:
Derivando essa expressão:
Obtemos então, que:
Passo 3
Em seguida, analisemos a condição em que o cursor desliza livremente sobre seu eixo na condição final. A energia cinética infinitesimal nesse caso é dada por:
E como temos a presença de duas barras agindo no noss sistema, com aceleração , chegamos até o seguinte fato:
Só que já sabemos que:
Obtemos então, que:
Passo 4
E a energia potencial presente da força elástica na condição final, que chamaremos de , em condições de deslocamento infinitesimal, é dada por:
Da figura do , tiramos que o deslocamente da mola vai ser dado por:
E consequentemente:
Logo, obtemos que:
Passo 5
Por fim, o que temos que fazer é igualar as energias final e inicial: