Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.7 - Ex. 165
A plataforma móvel de trabalho é elevada por meio de dois cilindros hidráulicos articulados nos pontos C. A pressão em cada cilindro produz uma força F. A plataforma, o homem e a carga têm uma massa combinada m e a massa do mecanismo é pequena e pode ser desprezada. Determine a aceleração ascendente a da plataforma e mostre que ela é independente tanto de b quanto de θ.
Passo 1
A partir do esquema disponível, é interessante a representação do diagrama dinâmico com as informações do sistema de coordenadas e parâmetros geométricos, dessa forma, tem-se:
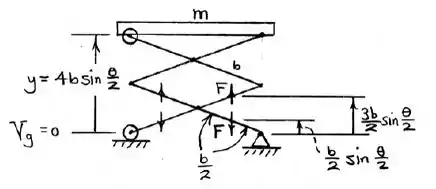
De forma diferencial, temos que:
Passo 2
A parcela da energia potencial será em termos diferenciais:
Passo 3
A parcela de energia cinética é quantificada da seguinte forma:
Passo 4
Assim, aplicando na equação global, tem-se:
Realizando as simplificações, pode-se obter a seguinte expressão:
Resposta
Pode-se demonstrar a independência do ângulo na determinação da expressão para averiguar a aceleração resultante do sistema, expressa por: