Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 28

Um bloco de 3 kg repousa sobre um bloco de 2 kg que está apoiado, mas não preso, a uma mola de constante 40 N/m. O bloco superior é subitamente removido. Determine (a) a velocidade máxima alcançada pelo bloco de 2 kg, (b) a altura máxima alcançada pelo bloco de 2 kg.

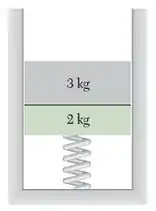
Passo 1

Opa!! Tudo blz? Neste exercício devemos calcular (item a) a velocidade máxima alcançada pelo bloco de 2 kg e (item b) a altura máxima alcançada pelo bloco de 2 kg.

(a) No ponto inicial, a força aplicada na mola é:

F m = m ⋅ g - k x

F m = 5 ⋅ g - 40 x

A máxima velocidade é

T 2 = 1 2 m 2 v 2

T 2 = 1 2 2 v 2 = v 2

U 1 → 2 = ∫ 0 x ( 5 ⋅ g - 40 x ) d x - 2 g x

U 1 → 2 = 3 g x - 20 x 2

T 1 + U 1 → 2 = T 2

0 + 3 g x - 20 x 2 = v 2

Como g = 9,81   m / s 2

v = 28,43 x - 20 x 2

Para a velocidade ser máxima, devemos ter

d v d x = 0

29,43 - 40 x 2 29,43 x - 20 x 2 = 0

x ( v m á x ) = 0,7358   m

Substituindo em 3 g x - 20 x 2 = v 2 , temos:

v m á x 2 = 3 ⋅ 9,81 ⋅ 0,7358 - 20 ⋅ 0,7358 2

v m á x = 3,29   m / s

(b) Agora iremos considerar a situação onde a mola está retornando após atingir a máxima velocidade.

x 0 = 2 g + 3 g 40 = g 8

F m = 5 ⋅ g - 40 x

U 1 → 3 = ∫ 0 g / 8 5 ⋅ g - 40 x d x - 2 g x 3

U 1 → 3 = 5 g 2 8 - 20 g 2 64 - 2 g x 3

T 1 + U 1 → 3 = T 3

0 + 20 g 2 64 - 2 g x 3 = 0

x 3 = 10 g 64

x 3 = 1,533   m

Resposta

( a )   3,29   m / s

( b )   1,533   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os pacotes são descarregados em um declive em A com velocidade de 1 m/s. Eles deslizam ao longo da superfície ABC para a esteira transportadora que se move com velocidade de 2 m/s. Sabendo que d = 7,5
Dois blocos idênticos são liberados em repouso. Desprezando a massa das roldanas e o efeito do atrito, determine (a) a velocidade do bloco B depois deste ter movimentado 2 m, (b) a tração no cabo.
Um caminhão-baú entra em um aclive com 2 % de inclinação deslocando-se a 72 km/h e atinge uma velocidade de 108 km/h em 300 m. O cavalo mecânico tem uma massa de 1.800 kg e o baú, 5.400 kg. (a) a forç
Um caminhão-baú entra em um declive com 2 % de inclinação deslocando-se a 108 km/h e deve reduzir para 72 km/h em 300 m. O cavalo mecânico tem uma massa de 1.800 kg e o baú, 5.400 kg. Determine (a) a
Dois blocos idênticos são liberados em repouso. Desprezando a massa das roldanas e sabendo que os coeficientes de atrito estático e cinético são μ s = 0,30 e μ k = 0,20 , determine (a) a velocidade do