Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 14

Os pacotes são descarregados em um declive em A com velocidade de 1 m/s. Eles deslizam ao longo da superfície ABC para a esteira transportadora que se move com velocidade de 2 m/s. Sabendo que d = 7,5 m e μ k = 0,25 entre os pacotes e todas as superfícies, determine (a) a velocidade do pacote em C, (b) a distância que um pacote deslizará na esteira transportadora antes de ficar em repouso com relação à esteira.

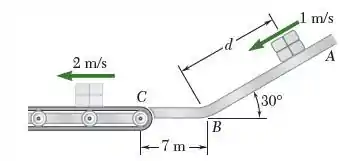
Passo 1

Opa!! Tudo beleza? Neste problema devemos encontrar a velocidade do pacote quando passa em C (item a) e a distância que um pacote deslizará na esteira transportadora antes de ficar em repouso com relação à esteira (item b).

(a)

Na parte inclinada da esteira, de A até B, temos o seguinte diagrama:

N A B = m ⋅ g ⋅ c o s 30 °

F A B = μ ⋅ N A B = 0,25 m g ⋅ c o s 30 °

U A → B = m g ⋅ d ⋅ s e n 30 ° - F A B d = m g ⋅ d ( s e n 30 ° - μ ⋅ c o s 30 ° )

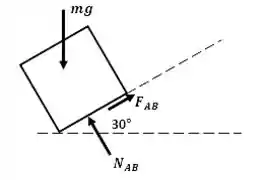
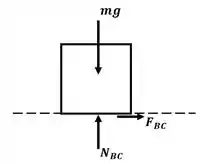
Para o nível de B até C, temos o seguinte diagrama:

N B C = m g

d B C = 7   m

F B C = μ ⋅ m g

U B → C = - μ ⋅ m g ⋅ d B C

Em A, temos:

T A = 1 2 ⋅ m ⋅ v A 2             e               v A = 1   m / s

Em C, temos:

T A = 1 2 ⋅ m ⋅ v C 2             e               v C = 2   m / s

Utilizando o princípio de trabalho e energia, e considerando que não há perda de energia em B:

T A + U A → B + U B → C = T C

1 2 ⋅ m ⋅ v A 2 + m g ⋅ d s e n 30 ° - μ ⋅ c o s 30 ° - μ ⋅ m g ⋅ d B C = 1 2 ⋅ m ⋅ v C 2

Dividindo por m e isolando v C 2 , temos:

v C 2 = v A 2 + 2 g d s e n 30 ° - 0,25 ⋅ c o s 30 ° - 2 μ g d B C

v C 2 = 1 2 + 2 ( 9,81 ) ( 7,5 ) s e n 30 ° - 0,25 ⋅ c o s 30 ° - 2 ( 0,25 ) ( 9,81 ) ( 7 )

v C = 2,9   m / s

(b)

Considerando d e s t como a distância que o pacote deslizará na esteira transportadora antes de ficar em repouso com relação à esteira, temos:

∑ F y = m a y

F x = μ ⋅ N = μ ⋅ m ⋅ g

Ao fim do deslizamento do pacote, temos v = v e s t = 2   m / s .

Utilizando o Princípio de trabalho e energia:

1 2 ⋅ m ⋅ v C 2 + μ ⋅ m ⋅ g ⋅ d e s t = 1 2 ⋅ m ⋅ v e s t 2

d e s t = v C 2 - v e s t 2 2 μ g

d e s t = 2,9 2 - 2 2 2 ( 0,25 ) ( 9,81 )

d e s t = 0,893   m

Resposta

(a) 2,9   m / s

(b) 0,893   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3/129) O pequeno cursor de massa m é liberado a partir do repouso quando na posição A e então desliza ao longo da pista no plano vertical. A pista Elisa de A até D e rugosa .(coeficiente de atrito din
3/139) A força P = 40N é aplicada ao sistema , que está inicialmente em repouso . Determine as velocidades de A e B após A ter se deslocado 0,4m .
3/141) Em um teste de projeto da pressão no anel de segmento , o pistão especial de alumínio com 100m m de diâmetro com uma massa de 2,7k g é liberado a partir do repouso no cilindro vertical sob a aç
3/138) O jogo de duas molas é usado para trazer o êmbolo A de 0,5k g para o repouso a partir de uma velocidade de 5 m / s e inverrter o seu sentido de movimento . A mola internaaumenta a desaceleração
3/140) O cilindro de 6k g é liberado a partir do repouso na posição mostrada e cai sobre a mola , que foi inicialmente pré-comprimida em 50m m pela trava leve e fios restritivos . Se a rigidez da mola