Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 19
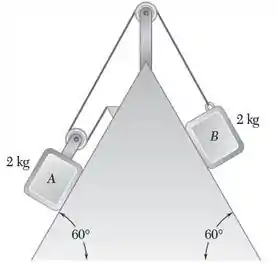
Dois blocos idênticos são liberados em repouso. Desprezando a massa das roldanas e o efeito do atrito, determine (a) a velocidade do bloco B depois deste ter movimentado m, (b) a tração no cabo.
Passo 1
Fala aê!! Tudo beleza? Neste problema devemos encontrar a velocidade do bloco B depois deste ter movimentado m (item a) e a tração exercida no cabo (item b).
(a) Considerando que o bloco B se moveu para baixo:
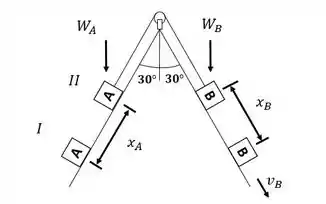
Como o trabalho foi positivo, B moveu-se para baixo, logo
(b)
Resposta
(a)
(b)
Exercícios de Livros Relacionados
3/142) Ensaios extensivos de um automóvel experimental de 900k g revelaram a força de arrasto aerodinâmico F A e a força total não aerodinâmica de resistência ao rolamento F R serem como mostrado no g
O carro de massa m acelera em uma estrada horizontal sob a ação da força motriz F de uma velocidade v 1 até uma velocidade mais alta v 2 em uma distância s . Se o motor desenvolve uma potência de saíd
O bloco de 10k g é liberado a partir do repouso sobre a superfície no ponto B , onde a mola foi esticada por uma distância de 0,5m a partir de sua posição neutra A . O coeficiente de atrito dinâmico e
Um menino de 40k g parte do repouso na base A de uma inclinação de 10 % e aumenta sua velocidade em uma taxa constante até 8k m / h quando passa em B , 15m ao longo da inclinação a partir de A . Deter
Um carro está viajando a 60k m / h descendo uma inclinação de 10 % quando os freios em todas as quatro rodas travam. Se o coeficiente de atrito dinâmico entre os pneus e a estrada é 0,70 , encontre a