Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 21
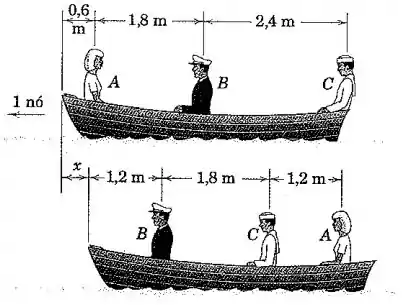
A mulher de , o capitão de , e o marinheiro de estão sentados no barco de , que está deslizando através da água com uma velocidade de nó. Se as três pessoas mudam suas posições conforme mostrado na segunda figura, encontre a distância do barco para a posição onde o barco estaria caso as pessoas não tivessem se movido. Despreze qualquer resistência ao movimento proporcionada pela água. Será que a sequência ou o momento da mudança nas posições afetam o resultado final?
Passo 1
Como não há forças externas, a quantidade de movimento do sistema é conservada, de forma que as velocidades inicial e final do barco são nó.
Porém, durante o momento de troca de lugar, as pessoas tinham alguma velocidade, de forma que a velocidade do barco sofreu alguma turbulência, resultando nessa diferença de deslocamento em relação ao referencial do barco se não houvesse troca de lugar, que se moveria com velocidade constante de nó.
Então, usaremos esse referencial que se move com velocidade constante para calcular a posição do centro de massa do sistema antes e depois das trocas de lugar. Como não há forças externas, essa posição do centro de massa deve ser constante, de forma que:
Passo 2
Então, vamos aos cálculos:
Portanto:
Como se vê, não precisamos de nenhuma informação sobre a sequência ou o momento da mudança nas posições para chegar a esse resultado, de modo que concluímos que essas coisas não afetam o resultado final. Beleza?
Resposta
Não