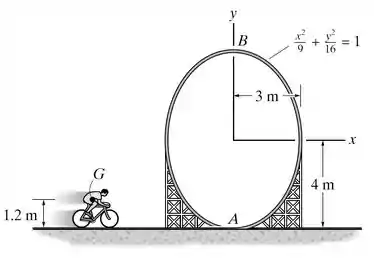
O homem na bicicleta tenta dar a volta no loop elipsoidal sem sair da pista. Determine a velocidade que ele tem de manter em A imediatamente antes de entrar no loop a fim de realizar a proeza. A bicicleta o homem tem massa de kg e um centro de massa de G. Despreze a massa das rodas.

pode ser determinado a partir da segunda lei de Newton para o momento em que a bicicleta passar em , de acordo com o DCL a seguir.

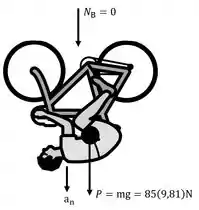
Como o raio de curvatura ainda é desconhecido, pode se determinar a partir de

Sendo que para a geometria para esta situação, temos:

O ângulo de inclinação no ponto B é dado por:

E o raio de curvatura no ponto B é:

m

Como o centro de massa do ciclista fica a 1,2 m da pista, o raio de curvatura do ciclista é:

m

Voltando para,

Pela figura a seguir é possível notar que a altura do centro de massa do ciclista no ponto B é m

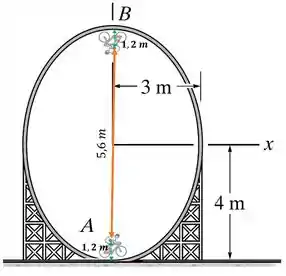
Aplicando a conservação de energia:

Então,